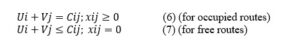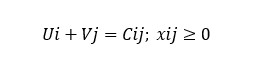Sustainable Development in the Global Distribution of Goods

Introduction

International freight transportation is an indispensable part of a contemporary economy of a country. Facing the growth and diversification of needs, international transportation is becoming a supreme necessity. The evolution of its volume influences the economy both at the state level and at the world economy level, becoming a component of major importance in international relations. The technologies in this area of expertise do not stand still, the results of the technical-scientific progress are intensively applied, meanwhile the main working directions being the optimization of the costs, the preservation of the qualities of the transported goods and the reduction of the transport duration.

The concept of sustainable development encompasses economic, social and environmental considerations that can evolve in interdependence, supporting each other, so that current generations can meet their needs without compromising the ability of future generations to meet their own needs (Hamuraru, Buzdugan, 2020).

Transportation, as a core component supporting the interactions and the development of socio-economic systems, has also been the object of much consideration to what extent it is sustainable (Schiller and Kenworthy, 2018). Sustainable transportation, as related McKinnon, et. al. (2013), is the capacity to support the mobility needs of a society in a manner that is the least damageable to the environment and does not impair the mobility needs of future generations. Sustainable development applied to transport systems requires the promotion of linkages between environmental protection, economic efficiency, and social progress (Rodrigue, 2020), Under the environmental dimension, according to Black (2010), the objective consists in understanding the reciprocal influences of the physical environment and the practices of the industry and that environmental issues are addressed by all aspects of the transport industry (McKinnon, 2018). Under the economic dimension, the objective consists of orienting progress in the sense of economic efficiency. Transport must be cost-effective and capable of adapting to changing demands (Noumen, 2019). Under the social dimension, the objective consists in upgrading standards of living and quality of life.

The classic transportation problem is part of the much wider class of problems that can be framed through transportation networks. A transportation network represents an economic situation in which, from a certain number of points, called sources, a quantity of a certain substance must be delivered to another number of points, called destinations. The extremely general situation from above can then be materialized in a particularly large number of ways, specifying whether there are intermediate points between sources and destinations, how the transportation is done (what are the possible routes, the cost of transportation, minimum limits and / or maximums for the quantity transported on each route, time required for transport), purposes pursued, etc. In the literature this issue is addressed by the authors: Gibbons (1985), Alexa (1995), Beck (2013), Lange (2013), Fujisawa (2015), Goosens (2015), Batkovskiy (2017) etc.

The physical distribution system, respectively the distribution logistics, is oriented to match the space and time that separates the production for consumption, through transportation and storage, referring to the physical flow of products from supplier to customer (Komlos J.,2019). Physical distribution is nowadays recognized as a strategic function, which, managed efficiently, is a source of both productivity-cost control and differentiation-quality and speed of response to user demand. In addition to these two functions, are mentioned as well the execution of orders and their delivery.

A completely separated approach to the two systems presented above is not justified because procurement and logistics activities have a lot of interrelated points, that are not taken over, except in some cases as different distribution compartments (Dima and Man, 2015). The efficiency of the distribution system increases when both areas of decision-making are applied simultaneously (Beck and Eldar, 2013). The choices made in the area of logistics, due to their direct impact on the price / service pair, are decisive for distributors.

Research question

Two hypotheses have been identified across transport problem research:

Hypothesis of sustainability: transportation optimization problems have been solved in way of sustainable development.

Hypothesis of cost optimization: the right management of the transportation costs aims for the right determination of the financial balance of the company.

Research design and methodology

The research complies with the following process: research and overview of the literature on sustainable transport development and on optimizing transport costs; applying the scientific research methods as comparative analysis, abstraction, minimum tariff method, North-West corner method and distributive method; processing and interpretation of the results. The presented data are based on the concrete aspects taken from the official sources of the Elégance Déménagement company (the subsidiary of the Republic of Moldova) and specialized bibliography.

Literature Review

This article focuses on the literature pertaining to supply chain management, transport and international expedition, sustainable transportation and optimization of goods transportation. It discusses the study’s theoretical basis, the concept of transport optimization problem and the opportunities of sustainable implementation, according to the Elégance Déménagement company example.

Transportation is one of the major components of the logistics system, due to its contribution to the fulfillment of the logistics mission, as we find in the book by Caraiani and Cazacu (1995). Transportation is often defined as the physical movement of people and goods between two points. In fact, the transportation of goods is a set of basic logistics activities, which occur in almost any marketing channel and consists in creating the utilities of place and time (Gross and Yellen, 1998). However, from a managerial point of view, transportation must be perceived as a system. Systemically defined, transportation represents the totality of resources (material, human, informational, financial) used in the realization of all processes (composed of physical and managerial activities), which lead to the transfer of goods and people (Voss, 1991). We narrow the scope from the level of the transport system to the level of the freight transport subsystem, which combines all the resources and processes that lead to the transfer of goods between two geographical points.

Thus, in this paper were addressed the theoretical notions related to distribution logistics and was presented the importance of logistics and its impact on companies. Logistics times were described, as well as the difference between traditional logistics and return logistics. The complexity of the classic parts involved in the transport of goods was noted. Mathematical models for optimizing transport costs were presented.

Results and Discussions

The transportation activities are carried out on a concrete territory and represent technologies and processes of movement of goods in space and time, which ensure various economic and production activities with raw materials, perform the storage of products and realization of finished products through means of transport.

Transport optimization problems are solved by applying mathematical models and methods, algorithms and programs to solve computer optimization problems, through automated processes of data collection and processing, the use of information and communication technology systems, which ensure achieving optimal control when moving means of transport (Radescu, 1990). The transportation activity is planned and directed according to several classical principles and modern management elements (Ilies and Crisan, 2010). Production entities plan in advance the volume of production to be carried out, the volume of raw material with which the undertaking is to be provided, the volume of storage and distribution, for the transport of which contracts are concluded with transport companies. Following these contracts, transportation companies plan their transport of goods for a long time, quarterly or monthly (Fred, 2011).

The main problems of efficiently using car transportation are solved in order to minimize the loaded routes, empty them or reduce to zero. The problems of minimizing the loaded journeys are solved by the economic agents, which aim to move the goods on short distances as possible, in order to diminish the influence of the transports on the freight costs, then the problems of minimizing the empty or to zero journeys are solved by the transportation companies. The first problems are solved in order to streamline production and logistics activities; the problems of minimizing zero and empty routes are solved to raise the level of efficiency of transportation activities.

The main purpose of the transportation activities is to increase the basic indicators for the operation of the means of transport which refer to the coefficients α (line emission coefficient), β (route utilization coefficient) and ɣ (load capacity utilization coefficient). Different mathematical models and methods are used to solve optimization problems in road transportation, which have three basic destinations:

• Problems in determining transportation plans in order to ensure the balance between transport capacities and volumes (maximizing the coefficient α)
• Problems in determining the efficient routes of direct transportation, distribution and collection of goods in small batches (maximization of the coefficient β)

3) Problems with the allocation of itineraries (routes) according to transportation companies, the distribution of the number of means of transport or the distribution of goods by available means of transport in order to use efficient means of transport when moving goods of different classes (maximizing the coefficient ɣ).

Another category of problems, which is solved for the efficient organization of freight transportation, is the distribution problems, the problems of collecting cargo in small batches. In such problems of optimization and operative planning of road transports, the values for all three basic indicators α, β and ɣ are maximized as a whole.

To determine the minimum transportation cost, we used linear models of transport type using linear programming in the optimization of the transportation plan (Balychev, S., et.al., 2018).

Formulation of the problem. In the management, organization and planning activity, there are a series of problems regarding the distribution of quantities from the supplying units to the consuming ones. Thus, for the elaboration of the internal transport plan at an enterprise, there is the problem of distributing certain quantities regarding a certain material from warehouses (suppliers), to production units (sections), workshops (consumers). This allocation must be made in such a way as to ensure minimum transport costs.

The general model of a transportation problem, when the existing one at the suppliers is equal to the necessary one at the beneficiaries (balanced type problem), consists of the following relations:

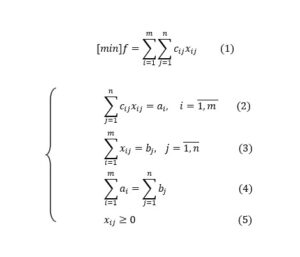
where:

a_i – existing quantities at the m suppliers;

b_j – necessary for n consumers;

x_ij – the amount of material transported from the supplier i and the beneficiary j;

c_ij– the unit cost of the material transported from the supplier i and to the beneficiary j.

Solving this transportation problem means finding from the set of the system of restrictions (2), (3), in the conditions of the relation (4), that solution that minimizes the relation (1).

Any set of values of unknown xij that satisfies the system of restrictions is called an admissible solution to the transportation problem. Any admissible solution that minimizes transportation costs is called an optimal solution. A solution to the transportation problem is called a basic solution if:

• It has at most m+n-1 strictly positive components, the others being null. Where m- number of suppliers, n – number of recipients.
• The columns corresponding to the non-zero components form an independent linear system.

A transportation problem is solved in two stages. In the first stage, an initial solution of the problem is determined, and in the case of the second stage, its optimization is performed.

Different methods can be used to determine a basic solution, such as: the North-West corner process, the maximum difference process, the minimum cost procedure, the minimum line element procedure, the minimum column element procedure.

For the optimization of the basic solution, in the second stage, several methods can also be used, such as: the distribution method, the potential method, the stepping-stone method.

To test the optimality of the solution, enter zero numbers Ui, called potentials Vj ∈ R.

Ui are the suppliers;

Vj are potential consumers.

The solution will be optimal if:

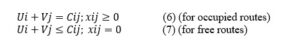
Different methods can be used to determine a basic solution, such as: The North-West corner procedure, the maximum differences procedure, the Minimum Tariff method, the minimum element per line procedure, the minimum column element procedure. To optimize the basic solution, in the second stage, several methods can also be applied, such as: distribution method, potential method, stepping-stone method.

From the listed procedures and methods, we will combine in the first stage of determining the initial solution the North-West method and the Minimum Tariff method, and in the second optimization stage we will perform the calculations by the distributive method, and at the end we will test the optimality.

The example of the company Elégance Déménagement is proposed as a case study. We consider a transport problem given by the following table, where the availability of suppliers, the need of the recipients and the unit transport costs (in euro) are presented. The problem is balanced. We will rate suppliers and recipients as follows:

95500 Gonesse, France → supplier A

77000 Melun, France → supplier B

93290 Tremblay en France → supplier C

72650 La Chapelle Saint Aubin, France → recipient 1

49000 Ecouflant, France → recipient 2

71000 Macon, France → recipient 3

Table 1: The availability of suppliers, the necessary units of recipients

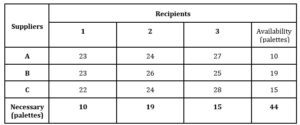
Source: Elaborated by the authors

Stage I

The use of the North-West corner or main diagonal method is shown in Table 2:

Table 2: Application of the North-West corner method

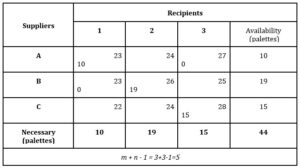
Source: Elaborated by the authors

From the analysis of the basic solution, it results that the number of occupied boxes is smaller than the one in relation (1.6), then it is necessary to fill in the free boxes with zero until the relationship is verified.

After obtaining the basic solution, the total transport cost to be performed is calculated by summing all the boxes in the matrix where quantities were distributed:

Total cost = 10×23 + 0×23 + 19×26 +0×27 +15×28 = 1 144 euro

The use of the Minimum Tariff method is presented in table 3:

Table 3: Application of the Minimum Tariff method

Source: Elaborated by the authors

From the analysis of the basic solution, it results that the number of occupied boxes is equal to the one in the relation m+n-1, which means that the problem can be solved.

Calculating the total cost:

Total cost = 10×22 + 10×24 +4×26 +5×24 +15×25 = 1 059 euro.

Stage II

The optimization of the initial solution proceeds until the optimal variant is obtained. The Minimum Tariff table applies, because the total cost is lower than in the North-West table. For this, we will apply the distribution method, according to which cyclic transfers of quantities distributed according to some contours polygons with right angles are performed, so that the sums of the quantities transferred on rows and columns do not change the total available per supplier and the total necessary to consumers.

Because there are as many possibilities to improve the basic solution as there are free boxes in the transportation plan matrix, the box with the greatest prospect of improvement will be determined in advance, by using the process of drawing up the free boxes’ cycles. In this sense, polygonal contours will be built, so that one corner is in a free box of the matrix of the transport plan of the analyzed solution, and the rest of the corners in boxes where there are already distributed quantities. At the polygonal contour thus formed, the + sign is passed in the free corner, and then, alternatively, the – and + signs at the other corners. With this, the corresponding costs will be passed in each corner as a rule, only a right angle can be formed in each box.

After constructing the polygonal accounts according to the mentioned rules, the algebraic sum of the distances from the corners is made, taking for each distance the sign of the corner where it is located. The box with the greatest prospect of improvement will be considered the one by which the algebraic summation of costs will have the greatest negative value.

For example, we start from the data presented in the table of the Minimum Tariff. As there are four free houses in this plan, four polygonal contours will be built according to the rules shown above, making the algebraic sum of the costs. Each box will be marked with a symbol representing the initial of the supplier, corresponding to the line on which the box is located, and the number corresponding to the consumer in the column on which it is located. For example, A-1 will symbolize the box on the line of supplier A and the column of the first recipient.

The box A-1 will be a rectangle with the corner in: A-1, A-2, C-1, C-2. The algebraic sum will be: 23 – 24 + 24 -22 =3

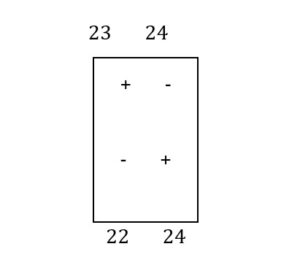
The box A-3 forms a polygonal outline with the tips in the boxes: A-3, B-3, B-2, A-2. The algebraic sum will be: 27- 25 + 26- 24 =4

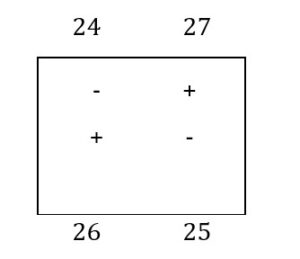
The box B-2 has a polygonal outline in the corners of the boxes: B-2, B-3, C-2, C-1. The algebraic sum will be: 23- 26 + 24- 22 = -1

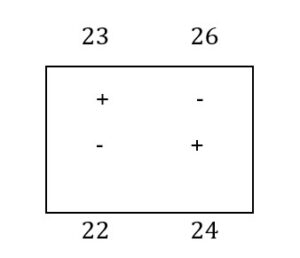
The polygonal outline of the C-3 box has the corners in C-3, C-2, B-2, B-3. Sum: 28- 24 + 26- 25 =5.

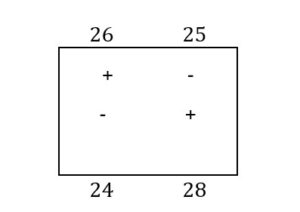
The analysis of the algebraic sums obtained for these four polygonal contours shows a negative value for box B-2. It means that this is the box with the greatest prospect of improving the transport plan. The basic solution is improved by performing cyclic transfers along the polygonal contour of box B-2. For this purpose, instead of costs, the corresponding quantities distributed through the basic solution of the transport plan, which need to be improved, are placed in the corners.

For the cyclic transfer proceed as follows:

• Analyze the size of the quantities at the corners with the negative sign of the polygonal contour, identifying the smallest quantity;
• Add to the existing quantities at the corners with the plus sign the minimum quantity from the corners with the minus sign, subtract this quantity from the corners with the minus sign;
• A new transportation plan is elaborated, in which the new quantities obtained by carrying out the cyclic transfer are passed in the boxes corresponding to the corners of the polygonal contour, all the other boxes remain unchanged, as in the basic solution;
• The transport cost is calculated on the basis of the new plan, which must be lower than in the previous version.

In this way, a new variant of transportation plan was obtained, which in turn needs to be improved. For this purpose, the same operations performed to improve the basic solution are used. The improvement of the transportation plan variants is carried out until the moment when, making the algebraic sum of the distances on the polygonal contour, no negative values are obtained.              

Continuing the analyzed problem, it turns out that B-2 is the box with the prospect of improving the transportation plan variant. Its polygonal contour is presented, passing instead of costs, the quantities corresponding to the boxes where the contour corners are located. He finds that at the corners with the negative sign, the smallest quantity is 4 palettes.

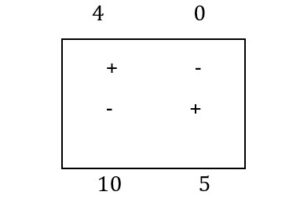
This amount is added to the corners marked “+” and subtracted at the corners marked “-“. In this way, a cyclic transfer of quantities is obtained, as shown in the polygonal contour, which is presented once again, but with the new quantities distributed at the corners.  

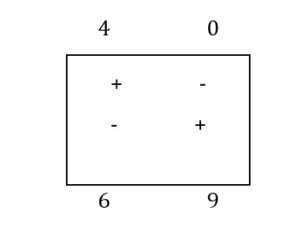
Depending on the new quantities, a transportation plan is drawn up in which the quantities obtained are entered; all the other boxes remain unchanged. The transportation plan obtained is presented in table 4:

Table 4: The transport plan obtained after the optimization stage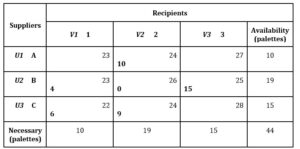

Source: Elaborated by the authors

The transportation cost after optimization is as follows:

4×23 + 6×22 + 10×24 0×26 + 9×24 +15×25 = 1 055 euro

Following the optimization calculations, we notice that the cost has been reduced by 4 euros. Next we will test the optimality of the solution.

For the occupied routes we form the system of equations:

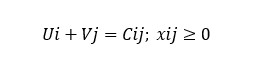
Because unknown elements we have 6, and equations only 5, then the system will be incompatible and indeterminate and we will get an infinity of solutions. To get a unique solution, we will consider that U1 = 0.

U1=0                                              

U1 + V2 = 24                                 V2= 24

U2 + V1 = 23     ⇒                        U2 = 1

U2 + V3 = 25                                V3 = 24

U3 + V1 = 22                                V1 = 22

U3 + V2 = 24                               U3 = 0

For the free routes we check the inequalities:

U1 + V1 = 0 + 22 = 22 ≤ 23

U1 + V3 = 0 + 24 = 24 ≤ 27

U2 + V2 = 1 + 24 = 25 ≤  26

U3 + V3 = 0 + 24 = 24 ≤ 28

So, following the calculations, we established that the transport cost of 1 055 euros is the best solution. Based on the description of the activities of organizing the distribution of goods within the company Elégance Déménagement were presented the service packages that the company provides to its customers, but also how to select vehicle planning before following transportation routes, how carefully each one is studied to know what type of vehicle should be engaged in transportation. In order to solve this problem, the mathematical model of the transportation problem was applied, in which the North-West corner method, the Minimum Tariff method, but also the distribution method was solved. All these methods have been applied in order to demonstrate how to optimize transportation costs in the distribution of goods. In this context, we recommend the company to follow this model in order to minimize the costs for the upcoming transportation activities.

Conclusions

Sustainable development involves establishing a balance between contemporary lifestyle and continued economic growth on the one hand, and environmental protection and finding alternative resources on the other. Public procurement is an innovative tool to support sustainable development at the level of the national economy, and the application of the methodology described by the authors, comes to support their development and will make it possible to assess the efficiency of public procurement and will also allow the identification of bottlenecks in the organization of public procurement while determining the efficiency of their use.

Distribution logistics consists of a set of activities that are closely related to each other, and they form an objective, to provide the customer with the desired product, in the right place, at the agreed time, in the required quantity and at the best rate. The purpose of distribution logistics is the realization, organization and delivery of goods from the supplier to the final consumer, in the shortest time, but also keeping the best conditions.

Transportation optimization problems can be solved by applying various mathematical models and methods, by using information and communication technologies in way of sustainable development. The efficient use of truck transport is solved in order to reduce empty or zero journeys, which produce costs and do not generate profit. The primary purpose of transportation activities is to increase the basic indicators during the operation of the means of transportation.

In order to optimize the transportation costs within the analyzed company, the transportation problem was applied in practice, in which we applied the North-West corner method, the Minimum Tariff method, the distribution method. With the help of this mathematical model, we were able to optimize transportation costs, which were initially higher compared to what we obtained from optimization.

It is not possible to draw a definite conclusion on a developing subject. Our study intended to highlight a new definition of the cost of transportation, which emphasizes the importance of different issues when moving a good, in condition to sustainable development. The right management of the transportation costs aims for the right determination of the financial balance of the company. Given that the company increases its profit from transportation services, a decrease in that transportation cost would generate a higher profit.  

Acknowledgment

Research and Innovation Project: – “Strengthening sustainable public procurement in the Republic of Moldova” 20.80009.7007.15, financed from the state budget within the State program 2020-2023.

References

• Alexa, C. (1995) Transports and international expedition, Ed. ALL, Bucharest.
• Balychev, S., Batkovskiy, A., Kravshuk, P., Trofimets, V. and Trofimet, E. (2018) ‘Situational modeling of transportation problems: applied and didactic aspects,’ Journal Espacios. 39 (no. 10) pp. 27-38.
• Batkovskiy, A.M., Semenova, E.G, Trofimets, V.YA., Trofimets, E.N., Fomina, A.V. (2016) ‘Method for Adjusting Current Appropriations under Irregular Funding Conditions,’ Journal of Applied Economic Sciences. Romania: European Research Centre of Managerial Studies in Business Administration, XI, 5(43), 828-841. https://www.ceeol.com/search/article-detail?id=534283
• Beck, A., Eldar, Y.C. (2013) ‘Sparsity Constrained Nonlinear Optimization: Optimality Conditions and Algorithms,’ Journal on Optimization Society for Industrial and Applied Mathematics, 23(3), 1480-1509. DOI: 10.1137/120869778.
• Black, W.R. (2010) Sustainable Transportation: Problems and Solutions, The Guilford Press, New York.
• Caraiani, Gh., Cazacu, C. (1995) International transports. Ed: Lumina Lex, Bucharest.
• Dima, I., Man, M. (2015) ‘Modelling and Simulation in Management Econometric Models Used in the Management of Organizations,’ Journal Contributions to Management Science. http://www.springer.com/series/1505
• Fred R. D. (2011) Strategic Management. Concept and cases. Francis Marion Univeristy, Ed: Pearson, Florence, South Carolina. 694 p. https://pracownik.kul.pl/files/12439/public/3_David.pdf
• Fujisawa, K., Shinano, Y. Waki, H., (2015) Optimization in the Real World: Toward Solving Real-World Optimization Problems. Springer. pp. 194-201.
• Gibbons, A. (1985) Algorithmic Graph Theory, Cambridge University.
• Goossens, F. (2015) How to Implement Market Models Using VBA. Wiley. pp: 312.
• Gross, L., Yellen, J. (1998) Graph Theory and its Applications, CRC Press LLC.
• Hamuraru M., Buzdugan A. (2020) Marketing compaigns to promote sustainable consumption. Primex-Com. Kishinow, 64 p.
• Ilies L., Crisan E., (2010) Goods transportation: concepts, internationalisation and management. Ed. Risoprint, 381p.
• Komlos J. (2019) Economics principles in a post-crisis world. Bucharest. Ed. Economica, 578 p. Lange, K. (2013) Optimization. Springer, pp: 540.
• McKinnon, A. (2018) “Balancing Efficiency and Resilience in Multimodal Supply Chains”, International Transport Forum Discussion Papers, Paris: OECD Publishing.
• McKinnon, A., M. Browne and A. Whiteing (2013) Green Logistics: Improving the Environmental Sustainability of Logistics, Second Edition, London: Kogan Page.
• Noumen R., Solutions de transport: les outils et les moyens de la logistique internationale, Montréal, les éditions JFD, 2019, p.215
• Pislariu, T. The QM software package – the transportation programme. EconPappers. https://www.rebe.rau.ro/RePEc/rau/jisomg/WI09/JISOM-WI09-A15.pdf
• Radescu, N., Radescu, E. (1990) Graph theory problem. Craiova, Ed. Scrisul Românesc.
• Rodrigue, J.P., (2020) The geography of transport system: Transportation, Sustainability and Decarborization, Fifth edition, New York: Routledge.
• Schiller, P.L., and J.R. Kenworthy (2018) An Introduction to Sustainable Transportation: Policy, Planning and Implementation, Routledge, New York.
• Voss, H. (1991) ‘Cycles and Bridges in Graphs,’ Journal Mathematics and Applications, East European Series, vol. 49. Kluwer.