This search is carried out through various services, which are typically Web Services. In order to automate the search, it must be taken into account that the input values of the Web Services are related. For example, in Figure 1, if the source city given to the Airplane Services (OA) differs from the source city (O), then it could be necessary to rent a car in order to reach OA from O. In other words, it is necessary to rent a car whose source city (ORC) is O and whose destination city (DRC) is OA. These form a set of constraints that relates the inputs of the various Web Services. Additionally, the goal of the user could be to attain the cheapest fare, in which case it would be necessary to minimize the total cost of buying an airline ticket and renting a car. In other words, this objective relates the output of the several Web Services.
Therefore, an optimization agreement between BPs based on Web Services is a special type of business process that is composed of a set of activities where: (i) each activity is based on a Web Service; (ii) there is no required sequence relationships between the activities; (iii) the activities have to achieve an agreement on the data input to obtain a common objective; and (iv) there may be a set of constraints that relates the input of activities, by restricting their possible values.
To the best of our knowledge, there are no solutions in the literature that enable this kind of problem to be described nor implemented in an automatic and graphic way. In this paper, a new methodology based on artificial intelligence techniques, and more specifically on constraint programming, is proposed in order to find those input parameters for each service that optimize the objective function.
The structure of the paper is organized as follows: Section 2 describes certain relevant related work. Section 3 lays out the type of problems to be solved in this paper and gives an illustrative example. Section 4 discusses how a Distributed Constraint Satisfaction Problem (DisCSP) can be used in the solution of optimization agreements in business processes by including certain related definitions, and explains the adaptation and improvement of certain algorithms for DisCSPs for optimization agreements in BPs. Section 5 presents the experimental results. And finally, conclusions are drawn and future work proposed in Section 6.
Related Work
The graphical standard for modelling business processes is Business Process Model and Notation (BPMN) proposed by the OMG (2009). BPMN can be used for a wide range of problems, mentioned by Wolter (2007). Furthermore, BPMN recently released Version 2.0 by the OMG (2011) for the solution of the majority of the modelling problems, however, remains as yet insufficiently powerful since, among other requirements, there is a significant need for the representation of the business process agreement in order to obtain an optimal solution. The Business Process Execution Languages for Web Services (BPEL) can represent the coordination where constraints are involved. Yunzhou et al. (2008) used a generalized adaptation and constraint enforcement models to transform the traditional BPEL process into an adaptive process. However, the authors solved the combined adaptation and constraint enforcement models in order to obtain a policy that recommends adaptive actions while respecting the constraints. Therefore, unlike this work,no agreement is made between activities.
Service-oriented systems have emerged as the paradigm to provide such automated support for business processes. Van der Aalst et al. (2003) and Papazoglou et al. (2007) presented Web Services as the infrastructure to foster business processes by composing individual Web Services to represent complex processes. Moreover, the coordination can be defined as a collaborative process, where the best service from among a set of existing and available services is chosen in order to fulfil the common need. Umeshwar Dayal et al. (2001) analysed and identified the requirements for BP flexibility in service composition and compared how existing process modelling and enactment approaches fulfil these requirements. However, in this work, each service that participates in the optimization agreement has an independent and distinct functionality. It is assumed that each of these services is the best at obtaining this functionality since the main objective in our work is that these services reach an agreement on the values of their input parameters. Therefore, the way that these best services are chosen from among various services that have the same functionality is irrelevant in this paper.
That is why, although there are several studies on the composition of services, to the best of our knowledge, none solves the type of coordination that this paper presents: an agreement between independent and passive Web Services on the values of their input parameters that optimize an overall objective.
In fact, there exist certain web pages that provide services similar to our illustrative example. In Expedia (2011) and Travelocity (2011), the user can search for a trip which includes flights, hotel and car rental. However, in both cases, the user has to provide specific values for the input data and cannot provide a variety options, and hence the search is only a request to the services of flights, hotel and car rental in a parallel way with these specific values. Moreover, the car rental is for use during the trip in the destination city, and not for use in travelling to another city to take a possibly cheaper flight from an alternative source city. The main difference is that the user provides, in this work, a range of possible values. To this end, the search is not as simple as a parallel request since, for the various services, it has to be decided which specific values of the input data would obtain the cheapest trip.
Formal Definitions
A formal definition is essential, since it enables the identification, description and definition of the type of problems that required the modelling of optimization agreements with interval data input in business processes.
There is no standard definition for optimization agreements in business processes. However, there are several definitions of agreements in business processes, whereby the most appropriate in this paper is:
Definition 1. An agreement in a BP is an arrangement between two or more activities/sub-processes of a BP that have to reach an understanding according to a common goal.
This understanding between activities represents, in this work, the specification of the values for the data input that the activities share. An optimization agreement in business processes can be defined when this agreement definition is applied, and an objective function to be optimized is specified. This implies that managers of certain activities have to work together to achieve and optimize a common objective. This is considered an optimization problem since it is necessary to determine the specific data input values for the various activities in order to obtain the best solution for a specific criterion.
Let an Optimization Agreement Component (OAC) be a BP whose activities (A1,…,An) are independent and there is no priority order between them. For each activity Ai, a set of activity data input variables (IAi) and a set of activity data output variables (OAi) are defined. Then, the following concepts are introduced for this OAC:
Definition 2. Process Data Input Variables (PDI): The set of variables that represents the data given by the user or another external process. Every variable xi Є PDI could have multiple values v(xi) Є D(xi), where D(xi) is the domain of xi (D(xi) is a finite set comprising all possible values that can be assigned to variable xi).
Definition 3. Activity Data Input Variables (ADI): The set of variables that represents the set of all the data input of the activities of the OAC.
ADI = Ui:1..n (IAi)
Definition 4. Constraints (C): The set of constraints C, where each Ck Є C relates a subset of variables (xk,…,xj) belonging to the union of the ADI and PDI sets. This set represents a subset of the Cartesian product D(xk) X … X D(xj) that specifies the permitted combinations of values for the variables xk … xj.
Definition 5. Activity Data Output Variables (ADO): The set of variables that represents the result of the execution of the activities (OAi).
ADO = Ui:1..n (OAi)
Definition 6. Objective Function (ObjFun): The global optimization function to be satisfied. This function is defined in terms of output values of services and their relationship, and can be maximizing or minimizing.
ObjFun = Opt (f (ADO))
Definition 7. Process Data Output Variables (PDO): The set of specific values for the PDI, ADI and ADO.
The result of an OAC is an assignment v for which each instance is a mapping that assigns an element v(yi) Є D(yi) to every variable yi Є PDO. This assignment v satisfies all the constraints belonging to C, such that < {yi1,…, yik },Ci> Є C iff <v(yi1,…,yik)> Є Ci and optimizes the global function ObjFun.
Trip Planner: An Illustrative Example
An example of an OAC is a BP based on Web Services for the organization of a trip presented by Yunzhou (2008). This process consists of three Web Services which perform a concurrent booking of an airline ticket, a hotel room and, if necessary, the renting of a car.
This is an example where there is no priority of any activity (based on Web Services) over any other, since the main purpose remains the definition of the best value for each variable within the ranges provided by the user. Those values that minimize the total cost of the trip are therefore taken as the best.
Therefore, the customer provides the source and destination city, and the possible dates. In order to obtain the cheapest trip, the customer can also provide a radius of locations by means of the maximum number of kilometres that the user is willing to drive either to reach a different departure airport or to travel from the arrival airport to the hotel location.
Hence, there are eight PDI with an associated interval domain given by the customer:
- (X1) DepartingFrom: the city where the user prefers to depart.
- (X2) GoingTo: the city where the user prefers to go.
- (X3) DepartDate: the day when the user prefers to depart.
- (X4) ReturnDate: the day when the user prefers to return.
- (X5) setDepartingFrom: set of possible departure cities. D1 = <margin to maximum distance>.
- (X6) setGoingTo: set of possible destination cities. D2 = <margin to maximum distance>.
- (X7) setDepartDate: set of possible departure dates. D3 = <top margin, lower margin>.
- (X8) setReturnDate: set of possible return dates. D4 = <top margin, lower margin>.
Three types of predefined Web Services are combined in order to perform the concurrent booking of an airline ticket, a hotel room and, if necessary, the renting of a car. Each activity (Web Service) calculates the price given the possible data input. In other words, the Activities (Ai) and their ADI (IAi and OAi) are:
- (A1) Airline Web Service: this calculates the price of an airline ticket given the following entries:
o Data Input (IA1): Airline.DepartingFrom, Airline.GoingTo, Airline.DepartDate and Airline.ReturnDate.
o Data Output(OA1): priceAirline
- (A2) Hotel Web Service: this calculates the price of an hotel booking given these inputs:
o Data Input (IA2): Hotel.Location, Hotel.CheckInDate and Hotel.CheckOutDate
o Data Output (OA2): priceHotel
- (A3) Car Rental Web Service: this calculates the price of renting a car. The customer can rent a car twice: to drive to the source airport from home and to drive to the hotel from the destination airport.
o Data Input (IA3): CarRental.DepartingFrom, CarRental.GoingTo, CarRental.DepartDate and CarRental.ReturnDate
o Data Output (OA3): priceCarRentalSource OR priceCarRentalDestination
Therefore, ADI = IA1 U IA2 U IA3 and ADO = OA1 U OA2 U OA3. The way of calculating each OAi will depend on the companies, destinations, dates, etc., which are internal and independent decisions. Althougb each Web Service may be organized internally in a different way, this does not affect the problem in any way.
The ObjFun of the BP is to minimize the cost of the trip, which includes the cost of buying an airline ticket, staying in a hotel, and, if necessary, the renting of a car.
ObjFun = min (prices = priceAirlineTicket + priceHotel + priceCarRentalSource + priceCarRentalDestination)
Furthermore, there is a set of constraints that the BP has to take into account to achieve the optimization agreement. These constraints relate only to the data input given by the user and the data input of the services. Some of the coordination constraints that describe the problem are defined below:
• The airline ticket departure and return dates have to fit in with the input data proposed by the customer.
(1) Airline.DepartDate = setDepartDate
(2) Airline.ReturnDate = setReturnDate
• If the source airport is not in the departure location (3) or the destination airport is not in the hotel location (4), then the rental of a car is necessary.
(3) Airline.DepartingFrom <>
DepartingFrom =>
CarRental.DepartingFrom = DepartingFrom &&
CarRental.GoingTo = Airline.DepartingFrom &&
CarRental.DepartDate = Airline.DepartDate &&
CarRental.ReturnDate = Airline.ReturnDate
(4) Airline. GoingTo <> GoingTo =>
CarRental.DepartingFrom = Airline. GoingTo &&
CarRental.GoingTo = GoingTo &&
CarRental.DepartDate = Airline.DepartDate &&
CarRental.ReturnDate = Airline.ReturnDate
• If the airport is located in the destination city (5), then it is unnecessary to rent a car in the destination city.
(5) GoingTo = Airport.GoingTo =>
Hotel.Location = Airline.GoingTo
Solving Optimization Agreements in Business Process Models
BPMN (OMG (2011)) does not explicitly consider mechanisms to represent optimization agreement requirements. In order to capture these requirements within the BP, there are further techniques to model and solve the optimization. An optimization agreement in a BP is formed by a set of Web Services whose objective is to determine the values of the variables within the possible domain in order to optimize the output. This problem is similar to a DisCSP, where the information is spatially and/or semantically distributed between several nodes where no single node has knowledge of the whole information nor of the behaviour of the other nodes.
Distributed Constraint Satisfaction Problem (DisCSP)
A Constraint Satisfaction Problem (CSP) consists of a pair (V, C), where V is a set of variables, each with a finite and discrete domain, and C is a set of constraints. The domain of a variable is a set of values, each of which can be assigned to the variable. Each constraint is defined over some subset of variables and limits the allowed combinations of variable values permitted in the subset.
Solving a CSP implies finding a set of assignments for the variables that satisfies all constraints. In certain cases, the objective is to find all sets of such assignments.
If an objective function is included in the CSP, it is transformed into a Constraint Optimization Problem (COP). Dechter (2003) defined a COP as a regular constraint satisfaction problem in which constraints are weighted and whose goal is to find a solution which maximizes the weight of satisfied constraints.
In this work, the relationships between the different Web Services which participate in a BP can be defined as a set of constraints where the input values of the services can be specified. If all the information were public and there were a predefined order among Web Services, it would be sufficient to build and solve a CSP which centralized everything in a single node.
However, generally the information belongs to various companies and is distributed across various systems. Therefore, although many problems can be formalized as a CSP, when the constraints and variables are divided into different nodes, and these nodes remain unknown to any individual solver, the problem cannot always be modelled with a conventional CSP and it becomes necessary to use Distributed CSPs (Hirayama and Yokoo (1997)).
There are several definitions for DisCSPs, but the main idea remains: a CSP where the set of variables and constraints of the problem are distributed between agents. Abril López et al. (2007) mentioned that these agents are responsible for solving their own subproblems and for coordinating with other agents to achieve a solution to the overall problem. The differences between the various definitions lie within the information held on each agent on DisCSP, whether private or public. Furthermore, constraint programming and its formalization of problems presents a large number of advantages and disadvantages, as shown by Cejudo and Martinez Gasca (2010).
Finally, a Distributed Constraint Optimization Problem (DCOP) is a DisCSP where an objective function exists for the optimization of the selection of one of the possible solutions. Unfortunately, the existing methods for solving DCOP cannot always guarantee the quality of the overall solution, especially if the agents operate asynchronously, as presented by Pragnesh et al. (2005).
Using DisCSP to Solve Optimization Agreements in Business Process Models
A customer makes a request to a Web Service with a specific need and this Web Service returns the best result to solve that need. This Web Service is internally a BP for which an agreement has to be reached between different related Web Services to satisfy the customer needs. This problem fits the formal definition presented in Section 3 since there are a set of Web Services, constraints relating their inputs, and an optimization objective. This section details how this BP can be modelled by using DisCSP.
As in CSP, an optimization agreement has a set of variables with domains and a set of constraints that relate these variables. However, the constraints that relate the data input and output of each Web Service remain unknown and are located in different systems. Hence the use of DisCSP becomes necessary. In DisCSP, the set of variables and constraints of the problem are distributed between a set of agents Ag1, …, Agn who are in charge of solving their own subproblems and must coordinate themselves with the rest of the agents to reach a solution to the global problem. In an optimization agreement, each agent Agi corresponds to a Web Service. In addition, the variables and constraints of each agent Agi correspond to all variables and constraints of the Web Services, thereby preserving its character as either public or private. Nevertheless, the agents in DisCSP are not only in charge of solving the constraints and instantiate the variables that only they know, but they also have communication tasks. The agents in DisCSP are able to initialize and maintain various conversations with the rest of the agents by exchanging messages. However, the Web Services have the ability to communicate only their results, since each Web Service receives a set of data and returns a result according with that data and its functionality. Therefore, although the algorithms for DisCSP cannot be used directly on BP, most of the advantages and disadvantages of DisCSP can be extrapolated to optimization agreements in business processes based on Web Services.
Activity Agreement Coordinator
In order to ensure that the Web Services not only carry out an instantiation of the variables that satisfies all constraints, but also searches for the optimal value of the objective function, a coordinator activity, called Activity Agreement Coordinator is necessary. This coordinator activity forms a sub-process (OMG (2011)) that contains knowledge of the whole problem: from the objective function to the accesses to the various Web Services needed. In addition, the Activity Agreement Coordinator is also responsible for executing the algorithm necessary for the assignment of values to variables. Each Web Service has certain input parameters; therefore this activity must provide such data to each service. The problem arises when the input data of the Web Services can be related and can even overlap. In the Trip Planner, the illustrative example, the constraint (5) relates Airline Web Service input data and Hotel Web Service input data since the destination of the airline ticket must coincide with the hotel location if this airline ticket destination is the one chosen by the customer. On the other hand, the objective function depends up on the output data of the various Web Services.
Therefore, all functionality is encapsulated in the Activity Agreement Coordinator, which is a process composed of an algorithm that instantiates the variables and calls the Web Services to obtain the values necessary for the calculation of the objective function. These Web Services are independent and are located on the internet (see Figure 2).
Figure 2. Activity Agreement Coordinator
Activity Agreement Coordinator Algorithm
The algorithm used by the activity coordinator should consider all possibilities and retain only the best result. Algorithm 1 is based on a DisCSP algorithm for the coordination of optimization agreements in business processes. This algorithm can be classified as a combination of Centralized and Synchronous Backtracking presented by Yokoo et al (2000) and (1998) respectively. It is centralized, since there is an Activity Agreement Coordinator who has overall knowledge of the problem and is responsible for organizing the different agents, taking control of the instantiation of variables (in order to prevent repetition of the same instantiation of variables), and for ensuring that the Web Services achieve the objective function. This algorithm is also synchronous since all Web Services run in parallel and remain in communication only when the Activity Agreement Coordinator needs to combine their returned values.
Algorithm 1: OAP Algorithm by Parody et al (2011).
1: V := List of ordered PDI and ADI variables {v1,…,vk} and their possible values {v1={val11, .., val1n}, …, vk = {valk1, …,valkm}}
2: C := A set of constraints (c1,c2,…,cj)
3: STAGE := A set of functions (Key, Value) where:
Keyi = {vi belongs to V} and
Valuei = {valix belongs to Vi}.
4: SOL := solution contains a list with the values of the PDI, ADI, ADO and PDO variables and the value of the objective function (ObjFun) associated to each of these values.
5: SOL_OP := The optimum solution so far (result).
6: forall v belongs to V do
7: forall val belongs to v and satisfy C do
8: STAGE:= (v,val)
9: if (forall v exists val in STAGE) then
10: OBJ := Calculate_Objective()
11: SOL:= STAGE and OBJ
12: if (isBetter (SOL, SOL_OP)) then
13: SOL_OP := SOL
14: end if
15: else
16: //Go line 21
17: end if
18: //Do backtrack if there are no more values for variable v
19: end for
20: //Terminate if there are no more values for variables even if there are some variables which have not been explored
21: end for
The key of the algorithm is in line 10, where the function that calculates the objective function (ObjFun) of the problem is invoked (Calculate_Objective()). Internally, this function is a BP which uses the Web Services in parallel and invokes them (with their corresponding ADI) in order to obtain their ADO values. Once the ADO values are obtained, the ObjFun is calculated.
The function isBetter (line 12) indicates if the best solution found so far (SOL) should be updated with the new solution found (SOL_OP). In the example, the function isBetter returns true if the value of the objective function in SOL is less than the value of the objective function in SOL_OP (SOL.OBJ < SOL_OP.OBJ).
In the same way as for the search space in DisCSP algorithms, the search space in Algorithm 1 also has a tree structure. The Agreement Coordinator Algorithm chooses the variable (belonging to PDI or ADI) to be instantiated at each level of the tree, by composing the new partial candidate. In addition, each branch of the tree is one of the possible values of the variable to be instantiated at each level. The various Web Services return the best solution according to the values once all variables are instantiated. Sometimes there is no solution since, for example, one of the services has no valid solution for the range of dates stipulated by the user. In that case, the user is notified through the return of an empty solution. On the other hand, if there are several optimal solutions, only the first one found is returned since the optimal solution is updated if and only if the new solution is better, and not if it is equally optimal.
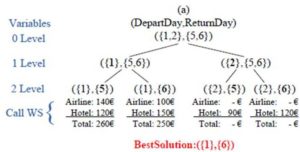
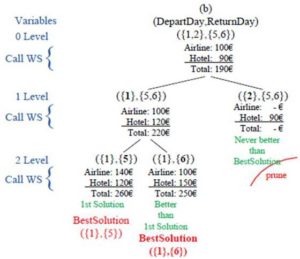
Following on with the Trip Planner example, the customer wants to buy an airline ticket to travel from Seville to London and to book a hotel in London. Moreover, to obtain the cheapest trip (ObjFun), the customer is flexible with the departure date: 01-07-2012 or 02-07-2012 and return date: 05-07-2012 or 06-07-2012. The Activity Agreement Coordinator executes Algorithm 1 (OAP Algorithm) and obtains the best solution, if it exists. The resulting tree structure is shown in Figure 3. In this example, there are four PDI stipulated by the user: DepartingFrom, GoingTo, DepartDate and ReturnDate, and the ADI (Airline Web Service input and Hotel Web Service input) will be instantiated from these PDI. However, since DepartingFrom and GoingTo already have specified values. and therefore, no domains, there are only two variables to instantiate: DepartDate and ReturnDate. At the beginning (0 level), both variables are non-instantiated, thus their domains still have all possible values. At the first level, the variable DepartDate is instantiated, since its domain has two possible values; there are two branches in the tree. And finally, at the second level, the variable ReturnDate is instantiated. The function Calculate_Objective() is called at this level since there is a complete assignment and therefore, all Web Services are also called.