Introduction

Warehouse management involves a huge quantity of product movements performed in a work shift, so its success depends on the procedure used to retrieve customer orders to deliver them on time at the lowest possible cost (Bustillo et al., 2015). Due to this fact, optimizing warehousing processes has become an important objective since a small efficiency improvement of these operations can produce significant savings in product movements and costs (Albareda-Sambola et al., 2009; Chen et al., 2005).

Order picking is the process responsible for recovering items from storage positions required by customer orders, minimizing costs related to traveled distance, operating time, and tardiness in the customer delivery (Albareda-Sambola et al., 2009; Azadnia et al., 2013; Bustillo et al., 2015). In addition, order picking is the most routine and labor-intensive process within warehouses, generating around 60-70% of the total operating cost (Chen et al., 2015), so significant reductions in costs can be achieved by applying efficient policies to retrieve items for customer orders (Albareda-Sambola et al., 2009; Chen et al., 2005).

For this reason, the order batching facilitates the order picking process by grouping customer orders in batches (Hsu et al., 2005), thus recovering several orders in a single tour and reducing traveled distances and by the warehouse (Chen et al., 2005). In this way, the items belonging to orders grouped in a batch are collected simultaneously, generating efficient picking routes (Albareda-Sambola et al., 2009).

The order batching is considered as an optimization problem that groups customer orders into a set of batches with a maximum capacity, and each customer order is made up of several items located in specific storage locations (Cano et al., 2018b). Therefore, the order batching aims to process a high volume of orders by consolidating small orders in batches, and prevails in warehouses to reduce the number of required tours, providing greater efficiency and productivity than using single-order picking (Bustillo et al., 2015; Chen and Shen, 2016). Accordingly, a batch is a set of grouped orders to be recovered in a single tour. In turn, a customer order is made up of a number of lines, and each line corresponds to an SKU, the requested quantities, and the storage locations to visit in a tour (Bozer and Kile, 2008).

Then, the picker routing problem determines the routes to retrieve the batches created in the order batching, and is considered as a Traveler Salesman Problem (TSP) (Cano et al., 2019a, 2019b, 2017a) that plans the shortest route to minimize travel distance and time, starting and ending in a point called Depot (Hsieh and Huang, 2011). As shown in Figure 1, usually a routing strategy is applied to determine the travel distance in each batch. Among these routing strategies, the most used in practice are the traversal or s-shape strategy and the largest gap strategy (Albareda-Sambola et al., 2009; Azadnia et al., 2013; Cano et al., 2017a, 2017b). Thus, the order batching efficiency is measured through the total traveled distance provided by the routing strategies.

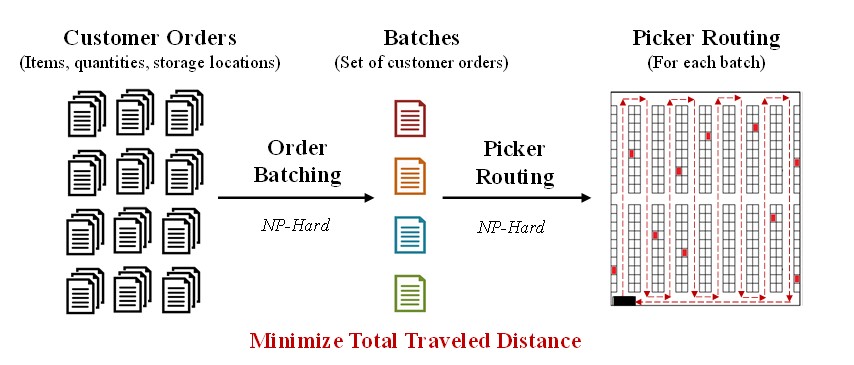
Fig. 1: Description of the OBP

On the other hand, the OBP is considered NP-Hard, which is why optimal solutions are difficult to obtain in reasonable computing times. Therefore, this problem can only be solved in polynomial time if each batch contains at most two customer orders (Gademann and van de Velde, 2005). To overcome these difficulties, some heuristics such as rule-based algorithms, and seed and savings methods have been proposed to solve the OBP (Albareda-Sambola et al., 2009; Hsu et al., 2005; Koch and Wäscher, 2016), as well as data mining methods, association rules and cluster analysis (Azadnia et al., 2013; Hwang and Kim, 2005).

In the daily operations of a warehouse, the order batching and picker routing must be performed frequently, so it is required to provide high-quality solutions (pseudo-optimal) without involving high costs in computational resources (Cergibozan and Tasan, 2016; Won and Olafsson, 2005). Therefore, it is essential to develop effective metaheuristic approaches such as Genetic Algorithms (GA), which are based on population search processes, evaluating several solutions simultaneously in each iteration, providing greater efficiency to find a pseudo-optimal solution (Cano et al., 2018a).

For the OBP, two genetic algorithm approaches have been used, which are item-oriented genetic algorithms and group-oriented genetic algorithms (Chirici and Wang, 2014; Koch and Wäscher, 2016). In item-oriented genetic algorithms, the number of genes in each chromosome is equal to the number of customer orders, so the size of the chromosomes is constant (Cano et al., 2018a); whereas in group-oriented genetic algorithms each gene represents a batch, so the size of each chromosome varies and depends on the total number of batches. However, one of the main difficulties in genetic algorithms is related to the choice of suitable parameters, because these parameters directly influence the algorithm’s convergence, the computing time, and the possibility of stagnation in local optima. It would be expected that the parameters could offer an adequate balance between exploitation and exploration of the solution space.

As shown in Table 1, some parameter values for item-oriented genetic algorithms in order batching problems have been proposed in the literature, as well as some parameter values for group-oriented genetic algorithms (see Table 2).

Table 1:  Parameters for item-oriented genetic algorithms

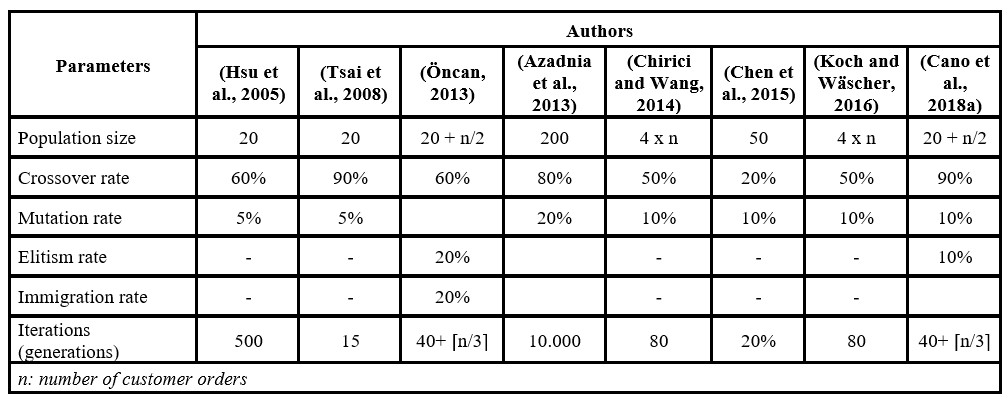
Table 2: Parameters for group-oriented genetic algorithms

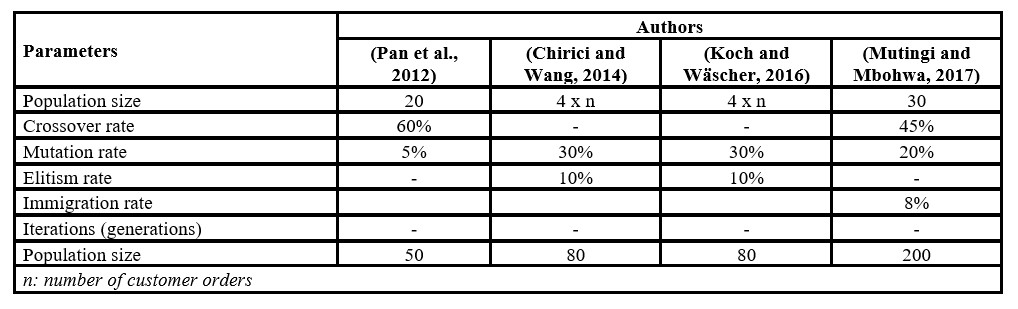
The information from Table 1 and Table 2 suggest the non-existence of standard values for genetic algorithm parameters, which invites to validate the parameter values for each OBP, taking into account the algorithm operators and specific programming conditions of each genetic algorithm. Therefore, this article aims to validate the parameters of a genetic algorithm for the OBP, identifying the parameter values that offer better solution quality and recommending strategies to reduce the computing time of the algorithm.

Genetic Algorithms for the OBP

Warehouses and distribution centers are interested in finding the most economical way to recover customer orders, which implies minimizing operating costs and reducing travel distance and time (Chen et al., 2005; Hsu et al., 2005). Thus, most of order batching problems focus on reducing the total traveled distance (Bozer and Kile, 2008, Chen et al., 2005, Hsieh and Huang, 2011, Hsu et al., 2005; Koch and Wäscher, 2016; Kulak et al., 2012), which also represents the operating costs reduction, and even the travel time reduction when considering constant speed for the picking devices. The assumptions for the OBP in warehouses and distribution centers are as follows:

• The size of a batch is limited by the capacity of the picking device.
• Each customer order is assigned to one and only one batch.
• A customer order cannot be assigned to several batches (no splitting).
• The size of a customer order is less or equal to the picking device capacity.
• The picker routing is performed in the first level of the warehouse, considering only horizontal movements.
• The tours performed to retrieve a batch follow an s-shape routing policy.

The use of group-oriented genetic algorithms prevails in recent years to solve the OBP since the representation of the solutions is aligned with the nature of the problem, encoding a batch into a gene. Using a group-oriented representation, the crossover operator will exchange batches (genes) between each pair of individuals selected as parents, transmitting genetic information to the next generations consistently with the problem to be solved. For the OBP it is more logical to exchange batches than customer orders.

Figure 2 shows the representation of solutions through item-oriented and group-oriented genetic algorithms. Based on a total of 10 customer orders, item-oriented approach always generates chromosomes of equal length (10 genes, one gene for each customer order), and a parallel chromosome representing the batch to which orders are assigned. On the other hand, a group-oriented approach generates chromosomes of variable length, which depends on the number of batches, and a parallel matrix showing the customer orders grouped in each batch.

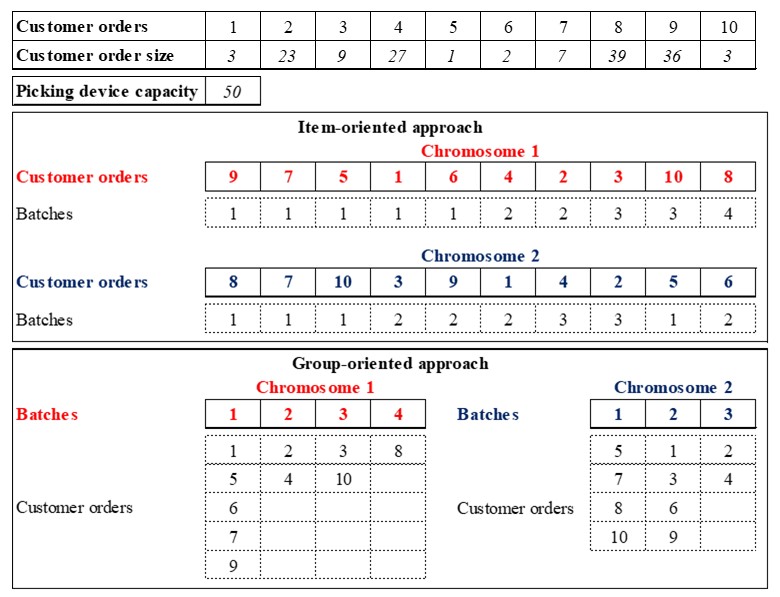
Fig. 2: Representation of item-oriented and group-oriented genetic algorithms

Moreover, a group-oriented genetic algorithm for the OBP works according to the following basic steps:

– Step 1: Set the population size (PS), number of iterations (NI), crossover rate (CR), mutation rate (MR), elitism rate (ER), and immigration rate (IR).

– Step 2: Create the initial population. Batch 1 is opened and assigned to the first gene, to which available orders are randomly assigned, and the assignment of orders is repeated until no order has a size less or equal to the available capacity of the picking device. Then, Batch 2 is opened and assigned to the second gene, repeating the customer order assignment process used for Batch 1. New batches are opened until all customer orders are assigned to a batch. This procedure to create genes (batches) is called Order Pool Procedure.

– Step 3: Calculate the fitness value of each chromosome using the s-shape routing policy for each batch (gene), providing the total traveled distance as the sum of the traveled distances in each batch. If the fitness value of the best performing individual in the current population is better than the overall fitness value, then the global fitness value is replaced by this fitness value and the global solution is updated.

– Step 4: Select the PS x ER best performing chromosomes and incorporate them into the next generation, guaranteeing the survival of the best-qualified individuals.

– Step 5: In order to select parent pairs, use the roulette wheel method to select PS x CR x 2 chromosomes randomly from the current generation.

– Step 6: Create PS x CR offspring using the crossover operator, and incorporate them into the next generation. A two-point crossover operator is utilized to exchange complete genes between parent chromosomes. To correct non-feasible chromosomes, old genes (batches) containing customer orders included into the new genes (inserted with the crossover operator) are deleted. The customer orders contained in the deleted genes become available in the order pool and are assigned to new batches following the procedure mentioned in Step 2.

– Step 7: Create PS x IR chromosomes for the next generation using the immigration operator, which is based on the same procedure used for the initial population in Step 2.

– Step 8: Randomly select PS x MR chromosomes from the new generation and apply to them the mutation operator. For the selected chromosomes, randomly select two genes and delete them. The customer orders contained in the deleted genes become available in the order pool and are assigned to new batches following the procedure mentioned in Step 2.

– Step 9: If the stop criterion is not satisfied, return to Step 3, otherwise, finish the algorithm and show the global solution and global fitness value.

Experiments

In order to establish the parameter values that provide a better performance in a group-oriented genetic algorithm for the OBP, the parameter values and operating conditions used by Chirici and Wang (2014), Koch and Wäscher (2016), Mutingi and Mbohwa (2017), and Pan et al., 2012 were taken as a reference for the experiments, as shown in Table 3. In addition, the experiments considered 50 iterations and the immigration rate (IR) was calculated as 1 – CR – ER for each experimental instance.

Table 3: Experimental values for genetic algorithm parameters

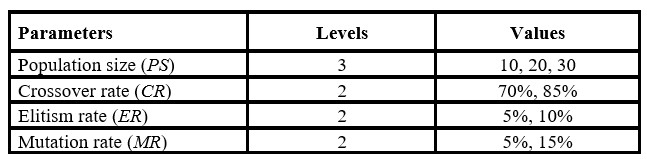
Therefore, 24 instances were generated, and 10 replications were run in each instance, obtaining 240 experimental runs to establish the parameter values for the genetic algorithm. As shown in Table 4, an operating environment was established according to the number of customer orders, the picking device capacity, customer order size, and the number of items per order.

Table 4: Experimental values for the picking parameters

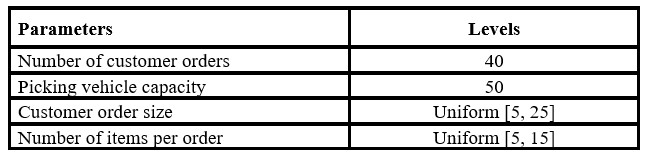
We used a warehouse with 10 aisles and 45 storage locations per aisle, for a total of 900 storage locations, following the same warehouse configuration used by Henn, (2015), Koch and Wäscher (2016), Menéndez et al. (2017a, 2017b), and Mutingi and Mbohwa, (2017).

Results

According to the experimental results, Table 5 shows that a population size of 20 individuals, a crossing rate of 85%, an elitism rate of 10%, a mutation rate of 5%, and an immigration rate of 10% provides the minimum total traveled distance for the group-oriented genetic algorithm. Results from Table 5 suggest that the genetic algorithm performance is enhanced using a high crossover rate, a higher elitism rate, and a lower mutation rate in order to promote better exploration of the solution space, guarantee in each generation the survival of the best individuals, and keep a low randomness level to avoid stagnation in local optima. Indeed, to include randomness to the algorithm, the parameter values prioritize the use of the immigration operator over the use of the mutation operator. Therefore, the randomness depends more on the creation of new individuals than on the alteration of specific genes in existing individuals.

Table 5: Performance of the genetic algorithm parameters

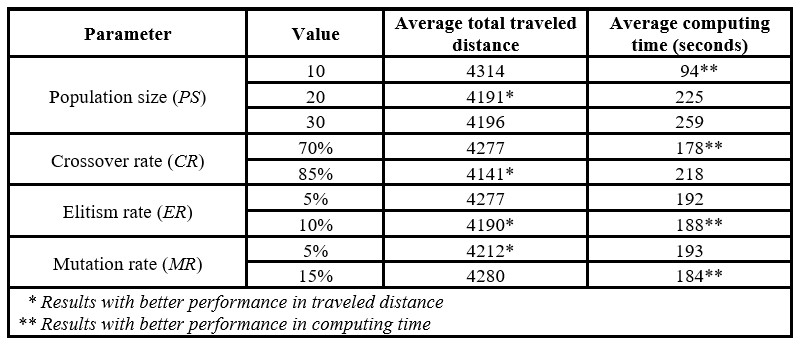
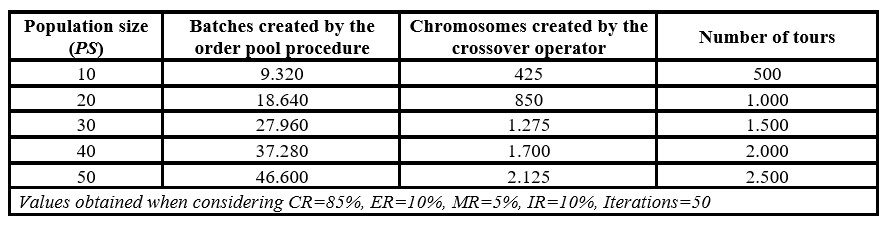
Regarding computing time, in almost all cases, the parameter values offering large traveled distance correspond to those offering shorter computing times. Therefore, according to the requirements of each OBP, decision-makers must establish a balance between the quality of the solution and the computational cost. For order batching problems demanding fast solutions, the population size (PS) should be reduced since this parameter is used for calculating the number of chromosomes to which crossover, mutation, elitism, and immigration operators are applied (see Table 6). Likewise, as the population size (PS) decreases, the number of tours performed with the s-shape strategy decreases. As the order pool procedure is used for the initial population, the immigration operator, the mutation operator, and the correction mechanism in the crossover operator, then the population size significantly influences the number of batches created in the genetic algorithm.

Table 6:  Size of the genetic algorithm according to the population size

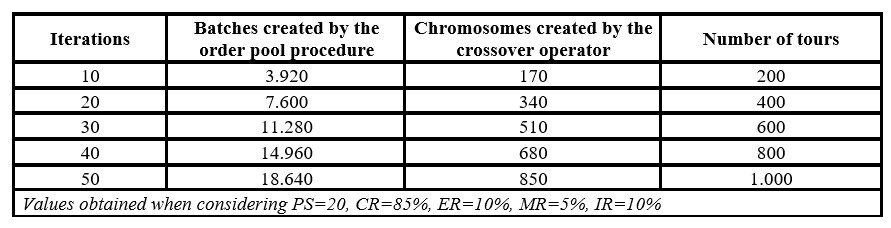
As a second option, the computation time decreases as the number of generations (iterations) decreases, so the number of steps of the genetic algorithm is drastically reduced. Consequently, the number of batches created by the order pool procedure, the number of tours, and the number of chromosomes created by the crossover operator increase linearly as the number of generations increases (see Table 7).

Table 7: Size of the genetic algorithm according to the number of iterations (generations)

Another strategy to reduce the computing time is including a stop criterion, so if a specific number of iterations is achieved without any improvement in the global fitness value, the algorithm finishes. Authors like Hsu et al. (2005) and Cano et al. (2018a) have proposed stopping the algorithm after 40 iterations without any improvement in the global fitness value, while Öncan (2013) proposes that this value is proportional to the number of customer orders, through the calculation ⌈n/4⌉, where n represents the number of customer orders.

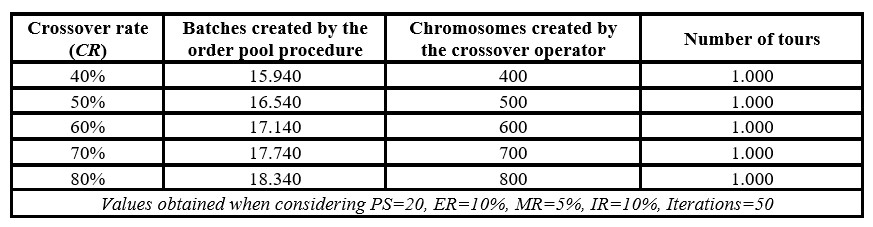
As a third option, the computing time of the genetic algorithm can be reduced as the crossover rate (CR) is reduced, decreasing the number chromosomes crossed in each generation, which usually requires a correction mechanism when the crossover creates unfeasible offspring (see Table 8).

Table 8: Size of the genetic algorithm according to the crossover rate

Finally, other strategies, such as including well-performing individuals to the initial population (solutions based on basic heuristics or priority rules), as well as the use of local search algorithms to refine the results of the best performing individuals in each generation, can increase the solutions quality and reduce the number of iterations required in a genetic algorithm.

Conclusions

This study defined the parameter values ​​for a genetic algorithm to guarantee better results during its execution in terms of the solutions quality and computing times. The parameter validation for a metaheuristic is required when an algorithm operator is included or excluded, when changing the solution encoding (item-oriented, group-oriented), and when adapting a metaheuristic used to solve other problems different to the OBP. For the group-oriented genetic algorithm addressed in this study, it is recommended to use a population size of 20 individuals, a crossover rate of 85%, an elitism rate of 10%, an immigration rate of 10% and a mutation rate of 5%. In case of requiring shorter computing times, we suggest reducing the population size and the number of iterations. Likewise, other strategies such as including well-performing individuals to the initial population and using local search algorithms could improve the solutions quality and computing time for a group-oriented genetic algorithm.

References

1. Albareda-Sambola, M., Alonso-Ayuso, A., Molina, E., De Blas, C.S., 2009. Variable neighborhood search for order batching in a warehouse. Asia-Pacific J. Oper. Res. 26, 655–683. https://doi.org/10.1142/S0217595909002390
2. Azadnia, A.H., Taheri, S., Ghadimi, P., Mat Saman, M.Z., Wong, K.Y., 2013. Order batching in warehouses by minimizing total tardiness: A hybrid approach of weighted association rule mining and genetic algorithms. Sci. World J. 2013, 1–13. https://doi.org/10.1155/2013/246578
3. Bozer, Y.A., Kile, J.W., 2008. Order batching in walk-and-pick order picking systems. J. Prod. Res. 46, 1887–1909. https://doi.org/10.1080/00207540600920850
4. Bustillo, M., Menéndez, B., Pardo, E.G., Duarte, A., 2015. An algorithm for batching, sequencing and picking operations in a warehouse, in: J.M., F., P., P.G., A., A. (Eds.), International Conference on Industrial Engineering and Systems Management, IEEE IESM 2015. Institute of Electrical and Electronics Engineers Inc., Seville, Spain, pp. 842–849. https://doi.org/10.1109/IESM.2015.7380254
5. Cano, J.A., Correa-Espinal, A.A., Gómez-Montoya, R.A., 2019a. Mathematical programming modeling for joint order batching, sequencing and picker routing problems in manual order picking systems. J. King Saud Univ. – Eng. Sci. https://doi.org/10.1016/j.jksues.2019.02.004
6. Cano, J.A., Correa-Espinal, A., Gómez-Montoya, R.A., 2018a. Solución del problema de conformación de lotes en almacenes utilizando algoritmos genéticos. Inf. Tecnológica 29, 235–244. https://doi.org/10.4067/S0718-07642018000600235
7. Cano, J.A., Correa-Espinal, A.A., Gómez-Montoya, R.A., 2017a. An evaluation of picking routing policies to improve warehouse efficiency. Int. J. Ind. Eng. Manag. 8, 229–238.
8. Cano, J.A., Correa-Espinal, A.A., Gómez-Montoya, R.A., Cortés, P., 2019b. Genetic Algorithms for the Picker Routing Problem in Multi-block Warehouses, in: Abramowicz, W., Corchuelo, R. (Eds.), Lecture Notes in Business Information Processing. Springer, Cham, pp. 313–322. https://doi.org/10.1007/978-3-030-20485-3_24
9. Cano, J.A., Correa-Espinal, A.A., Gómez-Montoya, R.A., 2018b. A review of research trends in order batching, sequencing and picker routing problems. Espacios 39, 3.
10. Cano, J.A., Gomez, R.A., Salazar, F., 2017b. Routing policies in multi-parallel warehouses: an analysis of computing times. Espacios 38, 23.
11. Cergibozan, Ç., Tasan, A.S., 2016. Order batching operations: an overview of classification, solution techniques, and future research. J. Intell. Manuf. 1–15. https://doi.org/10.1007/s10845-016-1248-4
12. Chen, M.-C., Huang, C.-L., Chen, K.-Y., Wu, H.-P., 2005. Aggregation of orders in distribution centers using data mining. Expert Syst. Appl. 28, 453–460. https://doi.org/10.1016/j.eswa.2004.12.006
13. Chen, N., Shen, C., 2016. A selecting method between picker-to-parts system and put system based on order cluster. Int. J. Control Autom. 9, 189–210. https://doi.org/10.14257/ijca.2016.9.7.18
14. Chen, T.L., Cheng, C.Y., Chen, Y.Y., Chan, L.K., 2015. An efficient hybrid algorithm for integrated order batching, sequencing and routing problem. Int. J. Prod. Econ. 159, 158–167. https://doi.org/10.1016/j.ijpe.2014.09.029
15. Chirici, L., Wang, K.S., 2014. Tackling the storage problem through genetic algorithms. Manuf. 2, 203–211. https://doi.org/10.1007/s40436-014-0074-1
16. Gademann, N., van de Velde, S., 2005. Order batching to minimize total travel time in a parallel-aisle warehouse. IIE Trans. 37, 63–75. https://doi.org/10.1080/07408170590516917
17. Henn, S., 2015. Order batching and sequencing for the minimization of the total tardiness in picker-to-part warehouses. Flex. Serv. Manuf. J. 27, 86–114. https://doi.org/10.1007/s10696-012-9164-1
18. Hsieh, L.-F., Huang, Y.-C., 2011. New batch construction heuristics to optimise the performance of order picking systems. Int. J. Prod. Econ. 131, 618–630. https://doi.org/10.1016/j.ijpe.2011.02.006
19. Hsu, C.-M., Chen, K.-Y., Chen, M.-C., 2005. Batching orders in warehouses by minimizing travel distance with genetic algorithms. Comput. Ind. 56, 169–178. https://doi.org/10.1016/j.compind.2004.06.001
20. Hwang, H., Kim, D.G., 2005. Order-batching heuristics based on cluster analysis in a low-level picker-to-part warehousing system. Int. J. Prod. Res. 43, 3657–3670. https://doi.org/10.1080/00207540500151325
21. Koch, S., Wäscher, G., 2016. A Grouping Genetic Algorithm for the Order Batching Problem in Distribution Warehouses. J. Bus. Econ. 86, 131–153. https://doi.org/10.1007/s11573-015-0789-x
22. Kulak, O., Sahin, Y., Taner, M.E., 2012. Joint order batching and picker routing in single and multiple-cross-aisle warehouses using cluster-based tabu search algorithms. Serv. Manuf. J. 24, 52–80. https://doi.org/10.1007/s10696-011-9101-8
23. Menéndez, B., Pardo, E.G., Alonso-Ayuso, A., Molina, E., Duarte, A., 2017a. Variable Neighborhood Search strategies for the Order Batching Problem. Comput. Res. 78, 500–512. https://doi.org/10.1016/j.cor.2016.01.020
24. Menéndez, B., Pardo, E.G., Sánchez-Oro, J., Duarte, A., 2017b. Parallel variable neighborhood search for the min-max order batching problem. Int. Trans. Oper. Res. 24, 635–662. https://doi.org/10.1111/itor.12309
25. Mutingi, M., Mbohwa, C., 2017. Optimizing Order Batching in Order Picking Systems: Hybrid Grouping Genetic Algorithm, in: Mutingi, M., Mbohwa, C. (Eds.), Grouping Genetic Algorithms: Advances and Applications. Springer International Publishing Switzerland, Cham, Switzerland, pp. 121–140. https://doi.org/10.1007/978-3-319-44394-2
26. Öncan, T., 2013. A Genetic Algorithm for the Order Batching Problem in low-level picker-to-part warehouse systems, in: Lecture Notes in Engineering and Computer Science. Newswood Limited, Kowloon, pp. 19–24.
27. Pan, J.C.-H., Shih, P.-H., Wu, M.-H., 2012. Storage assignment problem with travel distance and blocking considerations for a picker-to-part order picking system. Comput. Ind. Eng. 62, 527–535. https://doi.org/10.1016/j.cie.2011.11.001
28. Tsai, C.-Y., Liou, J.J.H., Huang, T.-M., 2008. Using a multiple-GA method to solve the batch picking problem: considering travel distance and order due time. Int. J. Prod. Res. 46, 6533–6555. https://doi.org/10.1080/00207540701441947
29. Won, J., Olafsson, S., 2005. Joint order batching and order picking in warehouse operations. J. Prod. Res. 43, 1427–1442. https://doi.org/10.1080/00207540410001