The Selection of Cost-Effective Transport Offers Using Genetic Algorithms

Introduction

Some of the most important aspects in the analysis of transport procedures are the administrative and legal aspects of freight forwarding. The increase in the number of freight forwarding companies specialising, today, in the securing of available transport offers and in obtaining the transport means to fulfil those offers is ever more apparent. This is an example of a typically specialised trade, within which management is mainly directed at sales. The situation is completely different in the case of those companies which combine freight forwarding with transport activities. For such companies, the key element is the planning process, the complexity of which is based on an increase or decrease in the number of transport offers at any given time in relation to the static number of transport means. This variability means that new methods, and consequently tools, are sought in order to support and automate the process of the allocation of transport means to transport offers for homogenous cargo. The issue at hand, therefore, concerns planning the best available solutions in order to support the decision-making process.  Another element is of importance here, in practical terms, namely the speed of such planning, that is to say, the shortest time required to determine the best solution [5]. For this purpose, genetic algorithms may be applied in an attempt to simulate possible populations in the computer’s memory when matching transport offers to available transport means. Such a population will generate many thousands of solutions for matching transport offers to the numbers of transport means available. The number of individuals is established on the basis of possible crosses, that is, new plans, or the re-planning of the same number of transport offers in relation to transport means. Additionally, the quantity and frequency of the various mutations should be considered, that is to say, the exchange of transport offers for others within the planning process.

Genetic Algorithms in Planning Transport Offers for Homogeneous Cargo 

The dynamics of changes on the transport market, in particular the constant introduction of new transport offers by parties making such offers and competing with other companies to secure them, disturbs the planning and managerial decision-making process. The many mutations, and particularly the vast growth in the number of individuals in the populations researched, arise mainly from the use of freight exchanges, which, for the majority of transport companies, are an additional and important source of obtaining transport offers [5]. Therefore, as a result of crosses and mutations, new solutions or individuals are created simultaneously with population increases. This growth is inversely proportional to the speed of finding acceptable solutions and slows down the decision-making process. In theory, a chosen parameter can be imposed on such a population, that is, a set of individual solutions, or otherwise manufactured plans for the completion of transport offers, which will narrow down the search and reduce the number of calculations. Economic parameters may be considered here, for instance the growth value or number of kilometres travelled without cargo, which cannot be higher or lower than the value calculated, using the analytical method within a given transport company. However, in practice, the majority of companies secure offers regardless of the economic parameter value, because the waiting time for a profitable offer is uncertain. Nevertheless, the entire crossing, mutation and selection process, is repeated indefinitely and constitutes the basis for the application of evolutionary programmes.

An evolutionary program is a probabilistic algorithm within which a population of transport offers, that is, individual offers, is generated, for each iteration, for example, after each mutation, that is, the exchange of transport offers secured for a freight exchange. Every plan for the completion of transport offers, that is, every individual, presents a possible solution for a task under consideration, vis-à-vis  the routes of transport means from the place of last unloading, to where the next load is to be taken on. Scheduled loading and unloading sites are represented in the programme by the -possibly complex- data structure ‘S’ which is a network of links to possible routes for the completion of transport offers. Each solution   is evaluated on the basis of a certain measurement of its adaptation, for instance, the shortest distance in kilometres, the lowest monetary costs and the time taken for the completion of any given transport offer as measured in hours. Therefore a new population, within the iteration t+1, is created by selecting those adopted transport offers, completion plans, or individuals which are best adapted to the work in prospect; this is the selection phase. Some transport offer plans, or individuals of a new population, also undergo a transformation, or a change phase through genetic operators, resulting in further, new solutions. They may be monadic that is, mutation types – the change of a transport offer within the planning process, within which new individuals are created by a small change to a single individual, or they may be polyadic transformations   of the crossing type within which new individuals are created, by combining, say, two or more parts of individuals, with the number of possible, acceptable solutions, that is– with the completion plans for accepted offers. After a few steps of generation, the programme merges and we expect that the best individuals represent a near optimum solution, that is, a justified and realistic solution). [1]

The Application of Genetic Algorithms

Taking into consideration that no sufficiently quick algorithms or methods for their solution have yet been developed for the class of issues related to the optimisation of transport offers obtained from freight exchanges, the authors of this paper took an interest in systems based on heredity. Bearing in mind that optimisation is one of the key fields for the application of genetic algorithms and also that many issues belong to the NP-hard class of issues, any concept for the most realistic and practically applicable solutions must, perforce, use probabilistic algorithms. The solutions adopted differ greatly from random algorithms, as they combine elements of a probabilistic and stochastic search. Genetic algorithms maintain the entire population of potential solutions, while other methods return only one point from the searched area [3], [4].

In the concept for the application of a genetic algorithm here presented, as with any other evolutionary programme, the following elements are used to manage transport offers (Figure 1):

1. Basic representation of potential solutions for a transport task.
2. Method of generating the initial population of potential solutions.
3. Evaluative function which fulfils the function of the environment and evaluates the solutions according to their adaptation.
4. Basic operators which influence the composition of the children population. Values of various

parameters of the use of genetic algorithms, that is, the size of the population, and the probability of using genetic operators.

Figure 1: Application of a Genetic Algorithm in Planning Transport Offers (own elaboration)

The feedback loop supports the decision-making process and allows the evaluation of many important practical situations in the process of transport management. These may include:

– changes to freight exchanges, such as when new offers become available, which may have the most favourable economic parameters in comparison to other transport offers under consideration;

– completion of long-term, ongoing transport offers and the allocation of transport means at a given time, to the region where they are most likely to be utilised;

– system for the operation of transport means which determines their availability at a given time and place.

On the other hand, the loop will significantly delay the working time of the evolutionary algorithm and thus reduce the flexibility of the tools used to facilitate decision-making.

Concept of the Structure of a Genetic Algorithm adapted to Determination of an acceptable Set of Solutions when planning Transport Offers

Planning integration – a single individual

The equivalent of a set of transport offers for transport means intended for completion per unit time is an individual. In the evolutionary algorithm, it is also called a chromosome. In the concept presented, the analysis is based on the issue of the shortest distance to the place where the transport offer commences. Travel, or the so-called “empty run”, is conditioned by an equal distribution of supply and demand, in time and space, on the transport services market. Searching for the shortest route is determined by economic factors. In practice, this issue is present within the majority of transport companies. However, in transport companies which have stable, ongoing transport offers, this ‘empty run’ problem is less visible and is often allowed for in the price of the transport offers. However, in companies which mainly use freight exchanges, the problem of travel is a very important dilemma factor in the decision-making process. The question arises as to whether it is worth accepting another offer from the freight exchange or wait for another, more economically advantageous offer, but with a different time perspective.

In the concept presented, the individual is basically the only element in the algorithm which varies depending on the different applications of the algorithms. Therefore, designing an individual constitutes the most important part when it comes to designing the whole genetic algorithm. Due to the uniqueness of the species, it is difficult to define a “golden rule” for designing an individual. Bearing in mind that multiple individuals, numbering maybe several dozens, hundreds or thousands participate in a genetic algorithm, individuals with a limited length of representation are sought after. The research carried out shows that the number of individuals is strictly limited by the amount of available computer memory, therefore the less the representation of the species, the greater the number of individuals which can participate in evolution and therefore the greater the chances of finding a global optimum increase. Apart from that, other elements of the algorithm, such as crossing and mutation, will work much faster, as the size of single individuals will be smaller. For that reason, an important issue when selecting the structure of the individual for the problem at hand is the possibility of taking limitations into consideration.

In the concept adopted, the individual is constructed using pairs of the vehicle number (transport means) and the offer number (transport offer) wherein offers are randomly selected and allocated to vehicles. In the meantime, in order to ensure higher efficiency, the structure within which pairs are kept is limited to a minimum. The principle has been adopted, according to which the individual is dynamically constructed for each algorithm request due to the possible change in the number of vehicles and the actual change in the number of offers. For the question regarding the shortest distance, it has been assumed that the length of the individual will be equal to the number of vehicles and to each of them, exactly one transport offer will be allocated (Table 1).

Table 1: Principles for constructing a Genetic Algorithm for an Individual

As a consequence of the assumptions adopted, two individual representation models were created, one allowing for incorrect solutions, meaning solutions within which an offer is repeated for one individual, with the result that a special function ensures that the offer is allocated to one vehicle only within a given individual.

Drawing the initial Population

In the concept presented, another step is the determination of the size of the population generated. If the population contains too few individuals, the algorithm may stop at a certain local minimum because any certainly acceptable solution will dominate the entire population even though that solution may not be the optimum solution. On the other hand, if the size of the population is too great, it decreases the working speed of the algorithm. In this case, the time spent in waiting for a response disturbs the decision-making process. Such delays, when using freight exchanges, may lead to the loss of transport offers. After determining the size of the population, all individuals are constructed. Due to the fact that the initial population should be as varied as possible, each individual should be constructed totally at random. Here, it is possible to see the advantage of binary representation, where regardless of the type of the issue, the newly created individual contains the n amount of randomly generated bits.  In the case of the representation of an individual in the structure, each of its fields should be completed separately.

In the algorithm presented, this stage consists of generating pairs of vehicles and offers in order to:

1. allocate one offer to each vehicle, where:

– the length of the individual is equal to one vehicle,

– subsequent vehicle numbers are entered into the structure of the individual.

In this case, the numbers of offers, such as routes and commissions, are randomly selected each time and allocated to a subsequent vehicle. At this stage, it is possible to allocate several vehicles to the same offer within one individual, under the supervision of a function which ensures that an offer appears only once within an individual

1. allocating all offers, where:

– the length of the individual is equal to the number of offers,

– during the first stage, as before, subsequent offer numbers are entered into the structure of the individual,

– empty spaces are filled randomly with available vehicles, using the limiting function which ensures that a vehicle is allocated to a given individual no more than three times,

– numbers of vehicles are also selected randomly and allocated to an individual offer. This stage is performed in the same way as in point a. 

The initial size of the population is defined as a parameter in the calculation process, within which all randomly selected individuals are evaluated.

Evaluation of Individuals

In order to evaluate individuals defined in this way, it is necessary to check how the actions of a given individual fulfil expectations and as a consequence, how advantageous the result represented by them is. In the case studied, an additional penalty function for breaches in limitations was introduced. This entails checking if the offer is present within an individual twice. For each parameter, a different function for evaluating the individual was implemented. During evaluation of the initial population, the first individual of this population is adopted as the model. The values of the evaluation function of subsequent individuals are compared with the evaluation of the model individual at each stage. Where the evaluation of an individual is found to be better, this automatically becomes the new model.

In the concept presented, three evaluation functions were constructed, which work in the following way:

1. Shortest distance – the distance between the site where the vehicle is located and the loading point is calculated. Before starting the genetic algorithm, a matrix of all possible distances is created, where the numbers in column format subsequently become offer numbers, and where numbers in rows subsequently become vehicle registration numbers. The alternative is to request information on all distances from the databases. Each offer, within an individual, should only be present once; if the sum of the distances is repeated, a high value, such as 2000, is added. This causes incorrect individuals to be evaluated significantly less favourably. When allocating all offers, it should be taken into consideration that distances will be calculated between the unloading part of one offer and the loading up part on another route taken by this same vehicle. Therefore, a matrix of distance is created, which characterises the individual and combines all possible offers (Table 2).

Table 2: Matrix characterising the Individual with regard to Travel Parameters calculated in km

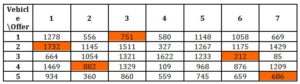
The evaluation of this individual is the total of the value of the cells highlighted in orange. The value of the evaluation function for this individual totals 4263, being the average distance to the loading point for a given individual. Within the analysis of the problem, if we adopt this solution as the model individual, then the objective function will need to be solved in a later iteration, where the average distance will be below the value of 4263 km for the individual studied.

1. The “full/empty” indicator is calculated on the basis of the analysis of distances and full runs according to the following rule: the number of kilometres travelled by the vehicle to the loading site in relation to the number of kilometres travelled throughout the entire offer. In the genetic algorithm presented, this indicator is calculated using the average of individual indicators from the entire length of the individual. In this case, the penalty function for repeated offers within an individual increases the value of the indicator by up to 100 %, which significantly lowers the result of the individual breaching the limitations (Table 3).

Table 3: Matrix characterising the Individual in relation to the “full/empty” Indicator calculated in %

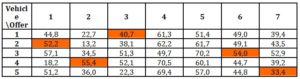
The evaluation function of this individual is the total value of the cells marked in orange. The value of the evaluation function for this individual totals 47,1%. As with the analysis of distances at point a, if the determined value of the “full/empty” indicator is adopted as the model, then it is expected to decrease in the following iterations.

Selection

The next stage of the application of genetic algorithms, in the concept presented, is the creation of a new population based on an existing one. Depending on the value of the evaluation function, as calculated at the previous stage, a given individual has better chances of being included in the next generation, if they are “good,” while they have poorer chances if they are “weak.” There are a few methods for calculating the “chances” of individuals. Belong to the:

1. Roulette wheel
2. Linear ranking
3. Tournament

The selection method is presented for example “Roulette whell”

In the classic genetic algorithm, the selection method based on the “roulette wheel” includes an n-fold random selection, n being the number of individuals from the old population of individuals which will be allocated to the new population. All individuals have various possibilities of being selected. This possibility is calculated using the following formula:

Adaptation Value of a given Individual / Sum of Adaptation Values of all Individuals

The above formula is only correct when the evaluation function is maximised. Taking into consideration the parameters adopted for the purpose of the analysis, that is, the shortest distance, or reducing the “full/empty” indicator, the evaluation function should be minimised.

Therefore, after conversion, the following calculation method has been proposed:

(Value of the worst Individual – Value of a given Individual + Value of the best Individual) / (Sum of the Values of all Individuals)

This solution reverses the evaluation function from determining the minimum to determining the maximum. 

In a case analysis, an individual may be drawn only once. In order to illustrate this likelihood, a table is created of the length of the sum of all adaptations, while the adaptation value is understood as the value of the parameter analysed, that is, the distance “full/empty” indicator. All individuals are entered into the number of cells equal to the difference between the worst adaptation and the adaptation of a given individual. The difference is increased by the value of the best individual so that the weakest individual also has a chance to go through to the next population.

Individuals will be sorted according to the function evaluating their best solution, that is, the smallest value of the parameter analysed

Example 1:

Table 4 : Genetic Algorithms in planning Transport Offers– Study on the Adaptation of Individuals

For a given population, the likelihood of the occurrence of adequately adapted individuals is calculated according to the following algorithm:

Number of Occurrences of studied Individuals = Adaptation (of the worst)- Adaptation(of a given Individual) +Adaptation of the best Individual.

Individual(1)= 6-1+1=6;

Individual(2)= 6-3+1=4;

Individual(3)= 6-4+1=3;

Individual(4)= 6-6+1=1;

On this basis, a possibility table for the adaptation of individuals is created:

Table 5 Genetic Algorithms in Planning Transport Offers – Table of the Probability of the Adaptation of Individuals 

The above table indicates the layout of the best of all the individuals drawn. Then, by using limitations, we can choose only those that will ensure adequate adaptations, in other words, the completion of previously defined parameters.

Crossing

The objective of the crossing phase is the exchange of so-called “genetic material” between two solutions or individuals, in a population. As a result of crossing, based on two planned transport offers in relation to two different available transport means, two new solutions or individuals are created. After crossing, new individuals replace previously scheduled ones in the population. Obviously, at this stage, not all solutions need to be crossed. The number of crosses is determined by the so-called crossing coefficient, at the value of between 0 and 1, which shows the number of individuals which should be crossed within one iteration or determines the likelihood of each solution being crossed. The presented concept uses two methods of crossbreeding:

1. Point selection crossing
2. Crossing by the Drawing of Offers

The crossing method is presented for example “Crossing by the Drawing of Offers”

This solution is different from the first as specific offers for exchange are indicated, with an exchange point being established subsequently in the population. The number of crosses between two individuals is drawn first. The next draw concerns offers within the two individuals, which will be exchanged. It is possible that an individual -after such crossing- will breach the limitations imposed. In this method, the programme can operate in two stages. In the first case, it can leave the individual in breach of the limitations and the penalty function will be imposed on it during evaluation. In the second case, the penalty function will cause another crossing at the point where limitations have been breached. All individuals may have various possibilities to breed. Therefore, each individual may have n number of offspring with various- or the same- individuals. Obviously, due to the calculation time of the genetic algorithm analysed, it is possible to determine, and therefore to limit, the percentage of crosses in relation to the entire population.

Example 2:

Table 6: Genetic Algorithms in planning Transport Offers – Crossing by drawing Offers 

Table 7: Genetic Algorithms in planning Transport Offers – Result of Crossing by drawing Offers at the Point of Breaching Limitations

In the case analysed, Table 7, those cells marked with the same colour were crossed in two individuals. This led to a breach of the limitations because within the second individual, two vehicles have an allocated offer with the number 10. Another crossing would be performed for the seventh vehicle of the second individual (Individual II) and any vehicle of the first individual (Individual I), except for those which have been crossed. The process will last until all vehicles within an individual are linked in accordance with free crossing.

Mutation

As with crossing, mutation ensures the addition of new individuals to a population. However, unlike crossing, in the case of mutation, only one individual is modified, not two. As with crossing, there is a so-called mutation coefficient, which determines how many individuals in one iteration will undergo mutation.

In the concept presented, a representative individual, and that part of it which is to be changed, is randomly selected. A number is randomly drawn from all offers and exchanged with the number of the position drawn. In such a mutation, an individual breaching limitations may also appear. All individuals from the entire population have the same chances of undergoing the mutation process. In order to limit the search, or calculation time, it is proposed to implement a method which does not breach the limitations imposed and an offer is selected for mutation only from the pool of offers not fulfilled by any given individual [2].

Example 3:

The mutation process may be performed in the following way:

Step 1:

Drawing an individual from the entire population (Table 8)

Table 8: Genetic Algorithms in planning Transport Offers – Selecting an Individual

to undergo Mutation 

Step 2:

Drawing part of the individual to undergo mutation (Table 9):

Table 9:  Genetic Algorithms in planning Transport Offers – Selecting an Offer to undergo Mutation

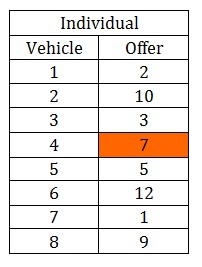
Step 3:

Drawing an offer from the pool of offers and exchanging it with an offer drawn in the previous step (Table 8):

Table 10: Genetic Algorithms in Planning Transport Offers

Mutation is important as it allows the introduction of new offers into the population, which may have been omitted over time. Thanks to mutation, the genetic algorithm is able to overcome local minima and reach the global minimum.

Conclusion

The concept presented here for the application of genetic algorithms for planning transport offers for homogenous cargo may constitute an example of solutions facilitating an increase in the economic efficiency of companies in the transport industry. Currently, only a small number of companies in this sector have a stable offer market for transport services. The dynamics and constant changes in the transport services market force transport companies to permanently search for new transport offers. Therefore, an enormous increase in the interest shown in freight exchanges is visible and these are starting to simulate and manage the supply and demand market of cargo transport. This situation creates an opportunity to seek new possibilities for increasing economic efficiency within the transport industry. This means that while having excess volume in transport offers, it is possible to increase the efficiency of the planning system from an economic perspective. For this purpose, various simulation techniques may be used, based among others, on the algorithms described herein. The authors of this paper propose an analysis of the indicators selected, namely, a reduction in distances and/or an increase in the value of the “full/empty” parameter, which have a significant influence on the profitability of transport offers and therefore on the increase in the economic potential of transport companies. The abovementioned indicators relate to the management method, wherein the main focus of the business model is the reduction in the costs of the services provided. For this reason, in the concept presented, travel to the loading point is the main source of the high costs of transport offers. In order to find an acceptable solution in the number of excess transport offers for homogenous cargo, with a limited transport means, the classic model of the evolutionary algorithm was used, as defined in Figure 1. The only limitation based on the research carried out was the analysis of homogenous cargo. In the case of heterogeneous cargo, an increase in the complexity of the calculations, with regard to time, should be expected in order to find acceptable solutions.

Application of genetic algorithms, with all their features for the creation of possible solutions, in order to evaluate the indicators under consideration may therefore be one of the tools facilitating decision- making in the process of the management of a transport company.

References

1. Davis, L., Steenstrup, M. (1987). Genetic Algorithms and Simulated Annealing: An Overview.

In L. Davis (Ed.), Genetic Algorithms and Simulated Annealing, pp. 1-11. Los Altos, Pitman, London. Morgan Kaufman Publishers Inc.

2. Gwiazda T.D. (2007), Algorytmy genetyczne. T. 1. Operator krzyżowania dla problemów numerycznych, Wydawnictwo Naukowe PWN, Warszawa.

3. Kierzkowski A., Zając M. (2012), Analysis of the reliability discrepancy in container transhipment, 11th International Probabilistic Safety Assessment and Management Conference and the Annual European Safety and Reliability Conference, p. 826-831.

4. Kwaśniowski S., Zając M., Zając P. (2010), Telematic problems of unmanned vehicles positioning at container terminals and warehouses, Transport Systems Telematics, Springer Berlin Heidelberg, p. 391-399.

5. Woźniak W., Wojnarowski T. (2015), A Method for the rapid Selection of profitable Transport Offers within the Freight Exchange Market, Amsterdam, The 25^th IBIMA conference on Innovation Vision 2020: from Regional Development Sustainability to Global Economic Growth.