Introduction
In practice, there is a broad spectrum of decision-making tasks, e.g. insurance business, economics, engineering, politics, etc., see e.g. (Dondi et al, 2014; Vats et al, 2014; Daniel et al, 2002; Hodouin, 2011; Maroney et al, 2008; Vasebi et al, 2012). These realistic decision-making tasks are often limited by available input information.
Extensive realistic industrial decision-making applications, such as chemical, petrochemical, food processes, are faced with the problem of inaccurate measurements, e.g. concentrations, flow-rates, etc., see e.g. (Thipwiwatpotjana and Lodwick, 2014). In practice, most factories are outdated and have therefore poor control systems that require an integration of vague heuristics and all available inaccurate measurements, see .e.g. (Dohnal and Sabadi, 2006).
Insurance business, economics and sociological / psychological decision-making applications are usually faced with vague, inconsistent input information, see e.g. (Daniel et al, 2002; Saïs and Thomopoulos, 2014). The same problem occurs when selecting new technologies based on appropriate and suitable criteria with respect to a particular developing country, see .e.g. (Vats et al 2014). Vague information is often described by fuzzy sets, see e.g. (Ciavolino et al, 2014; Yadav et al, 2014).
Most of the above noted decision tasks can be represented by single root trees, i.e. decision trees, and sets of available input information, such as probabilities, profitability, penalties, plausibility, etc., see e.g. (Thipwiwatpotjana and Lodwick, 2014). From the preceding text, it is apparent that there are two main problems (lack and uncertainty) of input information in the real-world., see e.g. (Kuzilek et al, 2014; Qin et al, 2014).
Lack of information is usually based on the usage of meta-heuristics; this is not the subject of this article, see e.g. (Bradshaw, 2000; Jegadeesh et al, 2004; Kubíčková et al, 2013).
Information uncertainty, i.e. there is unique, sparse, vague, partially inconsistent information, e.g. probabilities, profitability, penalties, etc., is a significant decision-making problem. Decisions are made under information shortage; therefore classical statistical methods are not applicable, see .e.g. (Spanos, 2010). If uncertainties cannot be quantified in a simple probabilistic way, then the topic of possibility decision theory is often a natural one to consider, see e.g. (Fargier et al, 2012; Dubois, 2014). In many studies, the problem of information uncertainty is handled using fuzzy sets, e.g. fuzzy numbers, see .e.g. (Dohnal and Sabadi, 2006; Dubois et al, 2013; Lee et al, 2011; Pedrycz et al, 2014; Zeinalkhani and Eftekhari, 2014).
The aim of this paper is to present an easy approach of how to identify profitability of the client in insurance business under the condition of input data uncertainty. The proposed easy approach is based on simulation method (Monte Carlo method), decision tree topology and experts’ estimates about probabilities and profitability.
The rest of the paper is organized as follows. The next section discusses the relevant methods. This section is followed by a case study. The final section presents some important issues and implications for future research.
Materials and methods
Creditworthiness criteria
In many insurance companies the profitability of the client is determined only by existing clients. The potential client is generally regarded as creditworthy. If there are the negative signals of the client then a detailed analysis is performed. This analysis includes evaluating the creditworthiness of the client’s particular client according to the following criteria:
Loss ratio is the ratio of the insurance claims and the earned premiums. Loss ratio is a very important factor in assessing the creditworthiness of the client. The higher the value of the loss ratio of the client is, the worse the creditworthiness of the client and conversely. In practice, The maximum value of loss ratio into 75% is often recommended. The client is unattractive over this value. The creditworthiness of the client is low and threatening in extreme cases his reject. It is necessary to add the next administrative costs (costs associated with the administration of insurance contracts and in particular their closure including the remuneration of intermediaries, etc.) in the amount least 20% to the value 75%.
Payment discipline is a historical view of the repayment premium. The insurance contract is terminated if the premium is not paying. The process of termination of the insurance contract shall be governed by the conditions laid down in the insurance contract. These conditions may be different in individual insurance companies.(Přečková, 2014)
Insurance penetration is the ratio of the insurance risks and the existing (real) risks. (Penetration is not understood in a macroeconomic sense as a ratio of earned premiums to GDP.) The higher the value of the insurance penetration of the client is, the better the creditworthiness of the client and conversely. (Shang and Chung, 2014)
Identifying the profitability of the client represents the process of evaluation of the pros and cons mostly by subjective opinions of the decision maker. This implies the risk of erroneous decisions caused by the human factor. The practical experience and the next abilities and skills of the evaluator in the decision problem occupied the significant role (Sun and Guo, 2013). Accuracy of this process has a direct impact on the marketing activities of insurance companies (Shang and Chung, 2014).
Decision tree evaluation
A decision tree has one root node, see e.g. node 1 in Fig. 1, where circles represent lotteries, boxes represent terminals and diamond represents a decision.(Rose, 1976; Welpe, 2014)
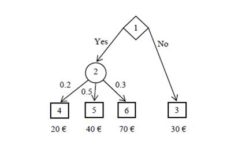
Figure 1: Decision tree (Source: own processing)
The following definitions are used below:
J Set of all decision nodes, see e.g. node 1, Fig.1.
I Set of all lotteries, see e.g. node 2, Fig.1. (1)
T Set of all terminals, see e.g. nodes 3, 4, 5 and 6, Fig.1.
Let us consider Si, for i ∈ I, is the set of all situations of ith node (lottery)
Si = {sik, k = 1, 2, … , K}, (2)
where K is number of all situation of ith node (lottery), see e.g. S2 = {s2k, k = 1, 2, 3} (branches 2—4, 2—5 and 2—6), Fig.1.
Situations (2) probabilities of ith node (lottery) is the column vector
p(Si) = [p(si1), p(si2), … , p(sik)]T, k = 1,2, … ,K, i ∈ I, (3)
see e.g. p(S2) = [0.2, 0.5, 0.3]T, Fig.1.
Valuation, e.g. profitability, all situations of ith lottery for certain decision node j is the vector
x(Si; j) = [x(si1; j), x(si2; j), … , x(sik; j)], (4)
where k = 1,2, … ,K, i ∈ I and j ∈ J, see .e.g. x(S2;1) = [20, 40, 70], Fig.1.
Valuation edges (branches) containing situation node is determined by an expected value, see (Welpe, 2014), of some random variable Z, e.g. profitability. This expected value can be written with relations (1)—(4) as follows:
E(Z|ji) = x(Si; j)-p(Si), (5)
see e.g. E(Z|12) = [20,40,70]-[0.2, 0.5, 0.3]T = 20-0.2 + 40-0.5 + 70-0.3 = 45, Fig.1.
Expected value (5) is compared with the valuation of edges (branches) without situation nodes, denoted xt for t ∈ T. Expected value E(Z|12) =45 € is greater than x3 = 30 €, according to the rule of maximizing profit, see (Welpe 2014), the decision is Yes.
Probabilities (3) and valuation (4) can be entered as experts’ estimates by lower and upper boundary, e.g. probability is from 0.15 to 0.25, profitability is from 30 to 45 €, etc. then expected value (5) is difficult to solve. Assuming that the probability and profitability is random variable, denoted V, then lower and upper boundary is
V ∈ [VL; VU]. (6)
The simulation method, e.g. Monte Carlo method, see (Tan et al, 2014; Chi and Beerli, 2014), may be used for determining (5). From interval (6), a value v is randomly generated and this value enters to relation (5).
Results
Case study describes the decision-making problem to extend or renew an insurance contract for next period (concretely two years). The solution of this problem is based on the decision-making task, which is graphically illustrated by a decision tree, see Fig. 2. The decision tree has five levels and three kinds of nodes — decision nodes (nodes number 1, 3 and 4), situation (lottery) nodes (nodes number 2, 5 and 6) and terminal nodes (nodes number 7, 8, 9, 10, 11, 12 and 13).
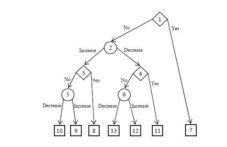
Figure 2: Decision tree (Source: own processing)
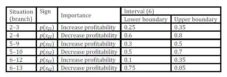
In the next table (Tab. 1) the importance of the main knots of the chart is described.
Table 1: Importance of branches (Source: own processing)
Decision nodes are nodes under management control, situation nodes (lotteries) are not under management control and terminals are possible results. The next table (Tab. 2) shows experts’ estimates (lower and upper boundary) of situations’ probabilities (nodes following the lottery).
Table 2: Probability estimates (Source: own processing)
The next table (Tab. 3) shows experts’ estimates (lower and upper boundary) of situations’ profitability (nodes following the lottery).
Table 3: Profitability estimates (Source: own processing)
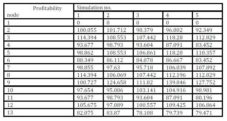
The following part presents the solving of the decision-making problem using Monte Carlo methods. For each situation, values of probabilities and profitability are generated, see intervals (6) Tab. 2 and Tab. 3. Generated values of probabilities form the vector (3), values of profitability form the vector (4). These vectors form the basis for calculating the expected values (5) of profitability of each decision node 1, 3, 4, see Fig. 1. The obtained expected values of profitability are compared with values of profitability x7, x8 and x11, see Tab. 3, which are generated too. This comparison leads to relevant decision. The above procedure is repeated 100 times. The first five simulations are shown in the next table (Tab. 4).
Table 4: First five simulations (Source: own processing)
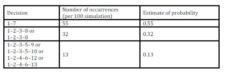
Table 5 shows identifying decisions and their estimates of probabilities. Decision 1—7 has probability 0.55, decision 1—2 has probability 0.45 (sum of 0.32 and 0.13).
Table 5: Profitability estimates (Source: own processing)
Because the probability of decision 1—7 is greater than decision 1—2, the final decision is the termination of the insurance contract in the first year. Minimum profitability value of this decision is 94.91 € and maximum value is 109.90 €. These values can be simply interpreted as follows; value of profitability can be expected with confidence 55 % from interval [94.91 €; 109.90 €].
Conclusion
The paper solves probably the most difficult decision-making problem related to the uncertainties of input information, namely the decision to extend or renew an insurance contract for the next period (concretely two years). The solution of this problem is based on the decision-making task, which is graphically illustrated by a decision tree. The main contribution of this paper is the easy approach of how to identify profitability of the client in insurance business under the condition of input data uncertainty. The proposed easy approach is based on simulation method (Monte Carlo method), decision tree topology and experts’ estimates about probabilities and profitability.
The advantage of this approach lies in the fact that it allows easy results for large decision-making problems under input information uncertainty. It also allows to simply incorporate risk aversion of the decision-maker, e.g. management and allows the decision-maker to have flexible control over decision-making problems and perform sensitivity analyses. The limitation of the proposed approach is the need to build decision tree (it can be large).
Acknowledgments
This paper was supported by grants FP-S-15-2787 “Effective Use of ICT and Quantitative Methods for Business Processes Optimization” from the Internal Grant Agency at Brno University of Technology.
References
1. Bradshaw, MT., (2000), How Do Analysts Use Their Earnings Forecasts in Generating Stock Recommendations? Social Science Research Network, Rochester, NY.
2. Chan, D.W/M., Chan, A.P.C., Lam, P.T.I., et al, (2011), ‘Risk ranking and analysis in target cost contracts: Empirical evidence from the construction industry‘, International Journal of Project Management, 29:751—763. doi: 10.1016/j.ijproman.2010.08.003.
Publisher – Googlescholar
3. Chi, H. and Beerli, P., (2014), ‘Quasi-Monte Carlo method in population genetics parameter estimation‘, Mathematics and Computers in Simulation, 103:33—38. doi: 10.1016/j.matcom.2014.02.005.
Publisher – Googlescholar
4. Ciavolino, E., Salvatore, S. and Calcagni, A., (2014), ‘A fuzzy set theory based computational model to represent the quality of inter-rater agreement‘, Qual Quant, 48:2225—2240. doi: 10.1007/s11135-013-9888-3.
Publisher – Googlescholar
5. Daniel, K., Hirshleifer, D. and Teoh, S.H., (2002), ‘Investor psychology in capital markets: evidence and policy implications‘, Journal of Monetary Economics, 49:139—209.
Publisher – Googlescholar
6. Dohnal, M. and Sabadi, R., (2006), ‘Fuzzy mass balances of sugar factory flowsheets’, INTERNATIONAL CONGRESS OF CHEMICAL AND PROCESS ENGINEERING. Prague, p P5.125.
7. Dondi, R., El-Mabrouk, N. and Swenson, K.M., (2014), ‘Gene tree correction for reconciliation and species tree inference: Complexity and algorithms‘, Journal of Discrete Algorithms, 25:51—65. doi: 10.1016/j.jda.2013.06.001.
Publisher – Googlescholar
8. Dubois, D., (2014), ‘On various ways of tackling incomplete information in statistics‘, International Journal of Approximate Reasoning, 55:1570—1574. doi: 10.1016/j.ijar.2014.04.002.
Publisher – Googlescholar
9. Dubois, D., Fargier, H. and Guyonnet, D., (2013), Data Reconciliation under Fuzzy Constraints in Material Flow Analysis. doi: 10.2991/eusflat.2013.4
Googlescholar
10. Fargier, H., Amor, NB. and Guezguez, W., (2012), On the Complexity of Decision Making in Possibilistic Decision Trees. CoRR arXiv: 1202.3718.
Googlescholar
11. Hodouin, D., (2011), ‘Methods for automatic control, observation, and optimization in mineral processing plants‘, Journal of Process Control, 21:211—225. doi: 10.1016/j.jprocont.2010.10.016.
Publisher – Googlescholar
12. Jegadeesh, N., Kim, J., Krische, S.D. and Lee, C.M.C., (2004), ‘Analyzing the Analysts: When Do Recommendations Add Value?‘, The Journal of Finance, 59:1083—1124. doi: 10.1111/j.1540-6261.2004.00657.x.
Publisher – Googlescholar
13. Kubíčková, A., Dohnal, M. and Doubravský, K., (2013), ‘Qualitative decision-making model of investment into start-up companies‘, International Journal of Technology Intelligence and Planning, 9:165—180. doi: 10.1504/IJTIP.2013.059656.
Publisher – Googlescholar
14. Kuzilek, J., Kremen, V., Soucek, F. and Lhotska, L., (2014), ‘Independent Component Analysis and Decision Trees for ECG Holter Recording De-Noising‘, PLoS One, 9:e98450. doi: 10.1371/journal.pone.0098450.
Publisher – Googlescholar
15. Lee, Y.C., Li, M.L., Yen, T.M. and Huang, T.H., (2011), ‘Analysis of fuzzy Decision Making Trial and Evaluation Laboratory on technology acceptance model‘, Expert Systems with Applications, 38:14407—14416. doi: 10.1016/j.eswa.2011.04.088.
Publisher – Googlescholar
16. Maroney, J.J., McGarry, C. and Ó hÓgartaigh, C., (2008), ‘Familiarity, home bias and investors’ reactions to 20-F reconciliation gains and losses and perceptions of the quality of accounting principles‘, The British Accounting Review, 40:103—122. doi: 10.1016/j.bar.2008.01.001.
Publisher – Googlescholar
17. Pedrycz, W., Al-Hmouz, R., Morfeq, A. and Balamash, A.S., (2014), ‘Building granular fuzzy decision support systems‘, Knowledge-Based Systems, 58:3—10. doi: 10.1016/j.knosys.2013.07.022.
Publisher – Googlescholar
18. Přečková, L., (2014), ‘How do insurance companies inform their clients of insured value within business insurance against natural disasters in the Czech Republic?’, Proceedings of 14th International Conference on Finance and Banking. Silesian university in Opava, Opava, pp 359—371.
19. Qin, G., Luo, L. et al, (2014), ‘Decision Tree Analysis of Traditional Risk Factors of Carotid Atherosclerosis and a Cutpoint-Based Prevention Strategy‘, PLoS One, 9:e111769. doi: 10.1371/journal.pone.0111769.
Publisher – Googlescholar
20. Rose, L.M. (1976) Engineering investment decisions: planning under uncertainty. Elsevier Scientific Pub. Co.”¯: Distributors for the U.S. and Canada, Elsevier / North Holland, Amsterdam; New York
21. Saïs, F. and Thomopoulos, R., (2014), ‘Ontology-aware prediction from rules: A reconciliation-based approach‘, Knowledge-Based Systems, 67:117—130. doi: 10.1016/j.knosys.2014.05.023.
Publisher – Googlescholar
22. Shang, Y.C. and Chung, C.L., (2014), ‘Appraising Marketing Performance for Insurance Businesses through Improved Fuzzy Modified GRA’, Journal of Grey System, 26:p96.
23. Spanos, A., (2010), ‘Statistical adequacy and the trustworthiness of empirical evidence: Statistical vs. substantive information‘, Economic Modelling, 27:1436—1452. doi: 10.1016/j.econmod.2010.07.007.
Publisher – Googlescholar
24. Sun, S. and Guo, W., (2013), ‘Research of Insurance Business Process Outsourcing Benefits, Models and Risks’, Proceedings of 2013 China International Conference on Insurance and Risk Management. Tsinghua University Press, Tsinghua, pp 208—214.
25. Tan, Y., Robinson, A.L. and Presto, A.A., (2014), ‘Quantifying uncertainties in pollutant mapping studies using the Monte Carlo method‘, Atmospheric Environment, 99:333—340. doi: 10.1016/j.atmosenv.2014.10.003.
Publisher – Googlescholar
26. Thipwiwatpotjana, P. and Lodwick, W.A., (2014), ‘Pessimistic, optimistic, and minimax regret approaches for linear programs under uncertainty‘, Fuzzy Optim Decis Making, 13:151—171. doi: 10.1007/s10700-013-9171-z.
Publisher – Googlescholar
27. Vasebi, A., Poulin, É. and Hodouin, D., (2012), ‘Dynamic data reconciliation in mineral and metallurgical plants‘, Annual Reviews in Control, 36:235—243. doi: 10.1016/j.arcontrol.2012.09.005.
Publisher – Googlescholar
28. Vats, S., Vats, G., Vaish, R. and Kumar, V., (2014), ‘Selection of optimal electronic toll collection system for India: A subjective-fuzzy decision making approach‘, Appl Soft Comput, 21:444—452. doi: 10.1016/j.asoc.2014.04.006.
Publisher – Googlescholar
29. Welpe, C.K., Straub, D. and Isabell, M. (2014) Risk – A Multidisciplinary Introduction. Springer
30. Yadav, J., Kharat, V. and Deshpande, A., (2014), ‘Fuzzy description of air quality using fuzzy inference system with degree of match via computing with words: a case study‘, Air Qual Atmos Health, 7:325—334. doi: 10.1007/s11869-014-0239-x.
Publisher – Googlescholar
31. Zeinalkhani, M. and Eftekhari, M., (2014), ‘Fuzzy partitioning of continuous attributes through discretization methods to construct fuzzy decision tree classifiers‘, Information Sciences, 278:715—735. doi: 10.1016/j.ins.2014.03.087.
Publisher – Googlescholar