Introduction
Our concern regarding the radio spectrum access began when we started asking questions about how different types of users can properly use the same limited resource. The dynamic behind this situation had to be well-organized and rigorously tested in order to become reliable for a community and be later extended at a global scale. With this idea in mind, we decided to explore the history of radio spectrum access and what it actually implies. The mathematical models provided a good insight into how the process functions at a core level and inspired us to think of a solution to the issues we stated in the beginning.
Short History
One of the main aspects regarding the extensive use of the wireless services from the last decade is that of the radio spectrum, which has gathered more and more attention in the last decade, having been studied by Han et al. (2012) as well as Bacci et al. (2015). Unlike most natural resources, the radio spectrum cannot be permanently depleted, however problems caused by its scarcity and access for users have risen. Therefore, of a particular interest for the wireless communication systems has become a term first proposed by Mitola and McGuire (1999), known as cognitive radio (CR). Considering the chance of better exploiting the spectrum holes, as was done by Weisz and Couch (2003), which occur especially in well-off urban areas, the cognitive radio network should allow both primary user (PU) and secondary user (SU) to share the spectrum in an efficient manner.
Due to the high demand for the radio spectrum, the Federal Communications Commission (FCC) replaced its former inflexible policies of “command-and-control”, allowing the wireless devices to operate dynamically. The importance of open sharing in unlicensed bands has greatly increased. For instance, Bluetooth devices, wireless computer networks (Wi-Fi) and near field communications (NFC) may use the ISM frequencies allocated for industrial, scientific, and medical purposes, as portrayed in the study by Sennouni et al. (2017). Nonetheless, in the absence of strict regulations, unlicensed sharing may cause overuse of the band, mutual interference, and considerable time delays for the transmitter-receiver pair. To avoid this “tragedy of the commons”, a term coined by Hardin (1968), basic protocols need to be established by an authority, either a government or an industrial committee.
With the aim of making the most out of the limited spectrum resources, fair sharing and efficiency constitute the main issue among multiple users. Several studies and papers have tried approaching this matter in various ways. Chandra and Keshavamurthy (2006) have analyzed access patterns of secondary users and how lowering the index of dispersion to a negative value has minimal effect on the primary users. Raman et al. (2006) have considered the possibility where a group of open links share a common spectrum, and a centralized spectrum server coordinates the transmission of this group. Yet, since multiple users are in a competition for a limited spectrum resource, we have no reason to consider them selfless. With the use of game theory, we can further analyze how these users may interact and seek an appropriate solution to the problem stated in the beginning. This branch of applied mathematics permits the analysis of the interactions between rational players (also called decision-makers) in order to achieve a common or conflicting objective. It is a flexible tool, very used in signal processing from beamforming for smart antennas and multimedia resource management to image segmentation and data security, as was proven in the study by Cao and Zheng (2005).
For example, a local bargaining strategy is proposed within the mobile ad-hoc networks. Multiple users self-organize into bargaining groups to reach a new optimal assignment while maintaining fairness among secondary users. In the study by Shum et al. (2007), a non-cooperative game had its premise consisting in investigating the iterative water-filling power allocation algorithm for Gaussian interference channels. A while back, Huang et al. (2006) described how a group of users who used a channel spread spectrum signaling, therefore generating interference with each other. Auction methods are proposed to allocate the received power among the users while the interference was kept below a certain value. However, since the users are competing for a limited spectrum resource, we should presume that they have no incentive to collaborate and thus render them as non-cooperative players. In the case of selfish users, a belief-assisted dynamic pricing approach was proposed in the experiment ran by Ji and Liu (2006), and double-auction rules are followed such that an overall efficiency of the spectrum and users’ incentives are maintained. A similar technique was used in another project by Ji and Liu (2006), where a system is also developed as a means of helping selfish users improve their strategies according to the network dynamics, thus substantially decreasing the pricing overhead. In the case of repeated games, it is more conclusive that a punishment mechanism is indeed efficient, as we can clearly notice in the book by Niyato and Hossain (2008), where multiple primary service providers are competing but are also compelled to keep their Quality of Service (QoS) constraints whilst selling their bands. Moreover, the experiment ran by Etkin et al. (2007) provides evidence that fairness and efficiency may be obtained with spectrum sharing rules and the best results are acquired in repeated games. By contrast, one-shot games provide not only unsatisfying results, but also raise a difficulty in applying a set of self-enforcing outcomes.
Aspects Regarding Games
Several dynamic spectrum access schemes with game theory as basis have been introduced and successfully implemented, notwithstanding there are still some questions that demand answers, as posed by Han et al. (2012) in their book. To begin with, the ever-changing spectrum environment has no central authority to control it, aspect which may pose some issues on the long run. As we can assume that the users have no incentive to cooperate, we may as well take into account the possibility of them giving or exchanging false information in order to gain a higher payoff. As a result, a cheat-proof scheme should be proposed for assuring an efficient usage of the sharing spectrum.
With these concerns in mind, in this paper we propose an intelligent system that will keep track of the number of games played, how the users choose to play and the winnings and losses that occur. Considering a repeated game, we suggest cheat-proof techniques for unlicensed users who will share the spectrum access. Punishment will be imposed if any user deviates from cooperation, aspect that may constitute the incentive they need to collaborate. We bring forward two strategies to avoid cheating: mechanism design and statistics-based strategy. Thus, users will be forced to cooperate honestly. However, the system mentioned above will also be responsible for sending private messages to each and every user proposing him the best response he should give according to his history.
The System Model
We examine a situation where N groups of secondary users exist in the same area and share a channel with the licensed user. Such is the case, for instance, when multiple devices connect to the same wireless network access point, such as a router. We are also aware that the users can communicate between them and will, unintentionally, produce interference to other groups. Further on, we consider N pairs of receiver and transmitter. Through a channel access method called CDMA (Code-division multiple access), at time t the unlicensed user receives a signal of the following form:

Where aj⌊ t ⌋ is the information that is transmitted,xj,i⌊t⌉ is the instantaneous channel gain from j to i (transmitter to receiver) and bi ⌈t ⌉ is the white noise received. Another assumption we make is that the channels are Rayleigh fading such that xj,t∼CN (0, aji2 ). The channels remain constant and from slot to slot change independently. We consider the white noise to be independently and identically distributed (i.i.d.) and N0 to be the noise power in wi ∼CN( 0,N0 ) .
In the proposed situation, we have a central unit that coordinates the spectrum access, but we have no guarantee that the transmitter-receiver pairs will cooperate. This is why we have to regard them as selfish, pursuing their own self-interest in the first place. Consequently, we bring forward the following model:
Players: N pairs of transmitters-receivers
Actions: each player chooses the transmission power level: Pi є [0,pimax]
Payoffs: Ri ( P1, P2.… …PN )gain of transmission achieved by player i after power levels P1,P2 … …PN have been chosen by each and every player.
In a general case, the gain of transmission is a positive increasing function of processed data.
The average payoff can be approximated as:
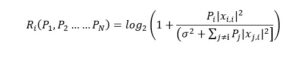
Where ó2 is the white noise treated with a Gaussian random variable.
a)Types of game
a)One-shot game
Regarding the one-shot game, we consider the players as caring only for the current payoff. We know that the vector of power levels (Pmax1Pmax2… … PmaxN)
is a Nash equilibrium thanks to the efforts of Wu et al. (2008). According to the formula above, as the fixed power level increases so will the average payoff. If any player decides to deviate from Pmaxi, there will be no equilibria, and considering that no player has any incentive to deviate from the best option for himself, it results that the only possible outcome for this game with selfish players can be expressed as follows:

During this one-shot game, the channel is heavily exploited due to the lack of cooperation among the players. With the purpose of maximizing their gains, players occupy the channel at a maximum transmission power. Therefore, interference will be felt by all participants at the game and the quality of the transmission they transmit decreases drastically.
- Repeated game
When it comes to open spectrum sharing, we need to regard the issues of not only constraining the players to respect the rules, but also encouraging them to cooperate. In the case of multiple rounds, ultimately seen as a game, the payoff is defined as the sum of transmissions:

Where δ ∈ (0.1) is called discount factor and Ri ⌊t ⌋ is the individual payoff at the time slot t.
b) Cooperation
Whereas in the one-shot game the cooperation is not a stable equilibrium, the opposite is true in the case of a repeated game enforced by the threat of punishment. More specific, if one of the players deviated from cooperation, there will be no more cooperation between the players, this threat being known as the “trigger” punishment. It has been proved that it is in the player’s best interest to cooperate so that the outcome is always beneficial, again, courtesy of experiments conducted by Wu et al. (2008).
While the utility of cooperation will be greater than the deviation one ( Ui cop> UI dev), any rational secondary user will maintain collaboration with the other users involved.
The major drawback of this approach is that it lacks efficiency and necessity. If a player deviates either on purpose or by mistake, not only he gets punished, but all the other players as well; therefore, the overall efficiency decreases. We need to rethink the purpose of the punishment. Preventing the deviating behavior is more important than the actual punishment; consequently, so long as the restriction imposed on the player makes him reconsider his choice, caring on with the punishment is no longer necessary.
Considering what we stated above, we propose a new strategy called “punish-and-forgive”. With this policy our aim becomes preventing rather than avenging uncooperative conduct. The game starts as a cooperative strategy and continues so long as no deviation is detected. However, when one player diverges from the initial approach, he will be penalized by the remaining secondary users from the group who will adopt the Nash equilibrium for the next time slots. After this time interval, the player is forgiven, and the cooperation is resumed. Here T denotes the duration of the punishment. The difference between the two stages in which a user may find himself cooperative versus non-cooperative is that while in the first case the spectrum is equally shared between the players and the quality of transmission is proper for everyone, in the second one, the state of the deviating user is similar to what a player tackles in a one-shot game thus the likelihood of interference increases considerably.
This time-limited punishment ensures a subgame perfect equilibrium. The latter term is a strategy profile in an infinitely repeated game if and only if no player can gain by changing his action after any history. At this point, we assume that our game is one with complete information: the utility functions, strategies, payoffs, and “type” of players are common knowledge. Such as the games with “perfect recall”, term introduced by Kuhn (1953), described as “equivalent to the assertion that each player is allowed by the rules of the game to remember everything he knew at previous moves and all of his choices at those moves”, the one concerning us operates in a similar manner. Nash equilibrium is achieved in every subgame, a game in its own right when seen in isolation from the bigger picture.
Further on we need to determine parameter T for the players that choose to deviate from the initial conditions. We know that cooperation guarantees an average payoff, an incentive for the player to cooperate. In addition, we analyze the end results from both types of strategies a player might choose, knowing that the expected utility of cooperation is greater than the deviation one.

Nonetheless, the selfish user has a motivation to seek a better outcome for himself rather than accept partnership. For this reason, T should be large enough to discourage any user from swerving. We denote as the maximum outcome obtained from deviation:

Regarding strategies
Cheat-proof strategies
So far, we assumed a repeated game with complete and perfect information. We are aware of the fact that information such as channel gains or transmission power level range is actually private, hence, nothing guarantees that the players will be honest in revealing their private information to the others. While cheating is profitable, we cannot assume that players won’t have any intention to cheat. Moreover, as the proposed rules may benefit the player with the best conditions, we can rightfully imagine that selfish players will exaggerate their situation so as to occupy the spectrum more often. Telling the truth becomes a crucial problem, so, measures have to be taken with the aim of creating an environment with equal chances for each and every player.
Mechanism Design Strategy
The first approach we suggest implies offering the users incentives to play honest. More specifically, the players who claim to have high values for the channel quality are asked to pay a tax which increases proportionally with the standards declared. As for the players with low quality mentioned, they will get monetary compensations. This strategy is based on the concept of transfer, term used in mechanism design, also known as reverse game theory. Now, the game slightly changes as the payoffs also include a monetary component which the players must take into account.
Being a coalitional game, players need to work together, and they do so by exchanging private information {φ1,φ2,φ3….. φk}. Let {φ1,φ2,φ3….. φk} denote the actual channel quality at one time slot. The secondary user reports φi , which may or may not be the same as φk. So {φ1,φ2,φ3….. φk}, is the common knowledge for all the users while {φ1,φ2,φ3….. φk} is not. In consequence, the transfer computation and allocation decision are based on presumably true rather than certain values.
The transfer of the secondary user in the proposed strategy can be written as:

Let be the notation for the sum of all the expected data throughput of the players if the player i attests a value of . Whether the user i chooses to claim a higher value of the channel quality than it actually is, the decision will reduce the general positive outcome the player intended in the first place. Declaring a channel value closer to the real one or even the precise one will overall be in the user’s advantage: despite occupying a smaller spectrum, the secondary user might receive an aforementioned compensation.
The experiments ran by Wu et al. (2008) have shown that the best decision a player can make is to tell the truth about their information. Starting on the grounds that one player chooses to deviate from the initial strategy, we know the only condition that maintains this course of action is that the payoff is greater than using the alternative. Thus, the equilibrium is reached when all players contribute in equal measure to the game.
Statistics-Based Strategy
The other strategy we are proposing implies an approximated proportional fairness. The latter term mentioned is an algorithm based on compromise, designed to maintain a balance between two competing interests: maximizing the total throughput of the network at the same time allowing the users to have a minimum service level. In the current proceeding, each user reports the normalized channel gain and the user with the highest value will get access to the spectrum. It is known that the normalized gains are exponentially distributed with a mean of 1, so, if players decide to be truthful, symmetry is thus achieved, as the spectrum is equally shared among the secondary users with each receiving 1/K fractional access.
With the aim of efficiently identifying the eventual cheaters, we designate η as a pre-determined threshold. If a player occupies more than (1/K+ η), there is a high possibility that a user has chosen to swerve from the opening state of the game’s assumption. Consequently, each player can access a maximum of 1 / (K+ η) of all the time slots. We note that so far there is no initial condition or supposition that the secondary users will not distort the information they are sharing.
The game proceeds as follows: a record is kept by each user marking the previous spectrum usages. If a player is discovered to exceed the imposed time limit, he will be catalogued as a cheater and punished. The profit of cheating is strictly connected to how much time passes between the maximum time allowed for individual usage of the spectrum and until the cheater is exposed. Therefore, the profit is bounded, the best value obtained being . Moreover, as the fraction 1 / (K+ η) tends to 0.
System Advice
The next issue we are going to address is the system we mentioned in the beginning of this paper. This system can be regarded as an algorithm-based program that comes as an additional aid to the original package of service. While the system doesn’t have access to the private information the users hold, it is highly aware of everything that happens as shared information and users’ responses. Our goal consists in reaching the Nash equilibrium in the shortest time frame possible at the same time without overloading the main system with unnecessary data. In order to facilitate this outlook, we suggest introducing this program only to secondary users, as they are the “guests” in the sharing spectrum and play a major part in our objective. The main characteristic of this program is its memory: it retains the past choices of each user and computes the current outcome after every round has taken place.
Firstly, the system will keep track of the games played and of the number of rounds. This means that it can correctly identify a game or a subgame in a specific time slot and understand when the game stopped, how much it lasted and what happened during the allocated time. Starting from the information it accumulated, we can begin analyzing what the players did throughout the time of a game. In the one-shot game situation, this system cannot be implemented, nevertheless, a kind message can be sent to all the secondary users asking them to collaborate for maximizing their gains. Persuasion brings better results in repeated games as there is an event history the system can examine. After the first round the system knows if the players chose to cooperate or not and it can respond accordingly. Should the users decide to work together, the system will send an encouraging message showing them the gains after each game. If the opposite is true, the system will ask the deviating players to be cooperative or else they will be punished.
Secondly, the program will be able to calculate the individual gains as well as the overall result, hence, it can make statistics of the evolution of the game in time. As we stated above, this intelligent structure will send for each player a message that besides the prepared supportive or warning text will also include a component concerning why partnership is essential and how on the long run this option is more profitable than the alternative. Further on, if the user collaborates, he will be shown the advantageous outcome he will benefit from, should he continue to do so until the end of the game. From another standpoint, for as long as the player deviates, the system will make a comparison between the current profit he obtains according to his choice and the estimated gains if he would cooperate on the whole unfolding of the game. By doing so, we are confident the users will eventually understand the convenience on the long-term collaboration and, more than that, also becoming aware that what is best for a group is also best for each and every member.
Conclusions
The spectrum is a limited resource which we aimed to use to its full potential by designing cheat-proof strategies to improve the efficiency and an intelligent system to keep track of the users’ progress. The sharing spectrum could be regarded as a repeated game where two cooperation rules were imposed one concerning mechanism design and the other being based on statistics. With productivity and fairness in mind, we designed these strategies to encourage players to avoid cheating, but if the case, apply punishment for deviating. Moreover, a perceptive system is proposed to aim at improving the performance of the spectrum usage and shortening the divergence time of the users. So far, our findings told us that it is better to try and prevent cheating in the first place rather than simply punishing where it is the case. However, the solutions proposed are mostly based on the idea that the various users will not try to cheat the system, which is not guaranteed. In addition, our solutions have not tested what could happen if all users happened to cheat, which only demands further study. We are certain that, given the time and resources needed, a more elegant solution to our problem will be found.
References
- Bacci, G., Lasaulce, S., Saad, W. and Sanguinetti, L. (2015), ‘Game Theory for Signal Processing in Networks’, IEEE Signal Processing Magazine
- Berry, RA. and Honig, M.L. (2006), ‘Auction-Based Spectrum Sharing by Jianwei Huang’, Springer Science + Business Media
- Cao, L. and Zheng, H. (2005) ‘Distributed spectrum allocation via local bargaining’, IEEE Communications Society Conference on Ad Hoc Communications
- Couch, LW and Weisz, WJ. (2003), ‘Radio Spectrum Utilization’, Encyclopedia of Physical Science and Technology, 3rd edition
- Etkin, R., Parekh, A. and Tse, D. (2007), ‘Spectrum sharing for unlicensed bands’, IEEE Journal on Selected Areas in Communications, vol. 25
- Han, Z., Niyato, D., Saad, W., Bașar, T. and Hjørungnes, A. (2012), ‘Game Theory in Wireless and Communications Networks: Theory, Models and Applications’, Cambridge University Press, ISBN 978-0-521-19696-3
- Hardin, G. (1968), ‘The Tragedy of the Commons’, Science Journal
- Jiu, Z. and Liu, KJR. (2006a) ‘Belief-Assisted Pricing for Dynamic Spectrum Allocation in Wireless Networks with Selfish Users’, Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks
- Jiu, Z. and Liu, KJR. (2006b) ‘Dynamic Pricing Approach for Spectrum Allocation in Wireless Networks with Selfish Users’, Proceedings of the Global Telecommunications Conference
- Keshavamurthy, S. and Chandra, K. (2006), ‘Multiplexing Analysis for Dynamic Spectrum Access’, IEEE Military Communications conference
- Kuhn, HW. and Tucker, AW. (1953), ‘Contributions to the Theory of Games’, Annals of mathematics studies, no. 28, vol. 2, Princeton University Press
- Lasaulce, S. and Tembine, H. (2011), ‘Game Theory and Learning for Wireless Networks: Fundamentals and Applications’, Academic Print, ISBN 978-0-12-384698-3
- Mitola, J. and McGuire, G. (1999), ‘Cognitive Radio: Making Software Radios More Personal’, IEEE Personal Communications, vol. 6
- Niyato, D. and Hossain, E. (2008), ‘Competitive Pricing for Spectrum Sharing in Cognitive Radio Networks: Dynamic Game, Inefficiency of Nash Equilibrium and Collusion’, IEEE Journal on Selected Areas in Communications, vol. 26
- Raman, C., Yates, RD. and Mandayam, NB. (2005), ‘Scheduling Variable Rate Links Via Spectrum Server’, IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks
- Sennouni, MA., Abboud, B., Tribak, A., Bennis, H. and Latrach, M. (2017), ‘Advance and Innovation in Wireless Power Transmission Technology for Autonomous Systems’, IGI Global
- Shum, KW., Leung, KK. and Sung, CW. (2007), ‘Convergence of Iterative Waterfilling Algorithm for Gaussian Interference Channels’, IEEE Journal on Selected Areas in Communications
- Wu, Y., Wang, B., Liu, KJR. and Clancy, TC. (2008), ‘Repeated Open Spectrum Sharing Game with Cheat-Proof Strategies’, IEEE Transactions on Wireless Communications, vol. VIII