Efficiency of Professional Polish Volleyball Clubs PlusLiga, Poland: Data Envelopment Analysis Approach

Introduction

This section should provide background of the study and highlight research motivation. In Poland, since the transformation of the economy after 1989, processes relating to the professionalisation and commercialisation of sport have been observed. These processes were the earliest to include sports clubs whose teams played in the highest competition classes. In 2010, Polish volleyball clubs, in agreement with the sports association, established a professional league, and to manage the competition, they set up Polska Liga Piłki Siatkowej S.A., which changed its name to PlusLiga SA in 2009. PlusLiga is the highest-ranked men’s volleyball league in Poland. The task of PlusLiga SA, which the clubs established, is to manage the league competition and sell media and centralised marketing rights. The clubs’ takeover of competitions organised by the sports association and all media and marketing rights give them a more significant say in critical matters. This includes the distribution of funds from selling sports match broadcasting rights. The disadvantages of such a solution may be that poorer clubs, where the primary source of funding is public money, fear that the professionalisation of the league and, thus, of the teams playing there will prove to be a challenge beyond their strengths. As a result of the club’s transformation into a company, they “enter” a higher level of organisational functioning in the professional sports market, where clubs may not be able to cope and, as a result, are at risk of losing financial stability.

Methods based on financial (indicator) analysis are often used to assess the efficiency of sports clubs. Very often, however, it turns out that more than an efficiency assessment based on an indicator approach is required. Sports clubs are specific organisations that differ from other enterprises that produce various goods and services regarding their objectives, legal form, organisational structure, and scope of operation. Clubs, especially those operating in limited companies, must pursue sporting and economic objectives (Sznajder, 2012). To gain a reliable understanding of the financial reality that characterises the functioning of sports clubs, it becomes necessary to search for and apply other methods to assess efficiency, mainly from fields such as statistics, econometrics or operational research.

This article aims to assess the degree of variation in the efficiency of the operation of volleyball clubs whose teams played in the 2020/2021 season in Poland’s highest phase of competition—the PlusLiga.

In this article, when talking about efficiency, we refer to the so-called technical (technological) efficiency in the sense of DEA, which is understood as the efficiency of transforming the inputs incurred by the club into economic and sporting effects (results). The efficiency of the clubs was established based on the non-parametric DEA method, and the input-oriented models, abbreviated CCR and BCC, were named after the first letters of their creators’ names.

The Concept and measurement of performance and the Production process of professional sports clubs – a review of selected literature

Efficiency is one of the basic categories used to evaluate an organisation’s activities. It is among the properties that determine its essence, condition its functioning and assess its development. The efficiency issue is highly complex in the literature due to the various definitions of economic efficiency. Samuelson and Nordhaus (2004) treat efficiency as the maximisation of production resulting from the proper allocation of resources under given constraints of supply (i.e. costs incurred by producers) and demand (i.e. consumer preferences). According to Cameron (1986), defining efficiency is highly complicated, but it is always necessary to refer to internal and external evaluation criteria specific to a given context and changing over time. Efficiency in economic science is considered in two dimensions: financial and organisational. The first dimension is related to efficiency research in economic theory. The second is related to management science and is the category of the synergetic effect of organisations, i.e. the benefits arising from specific arrangements of interaction within organisational systems. According to Matwiejczuk (2000), the concept of efficiency refers to the principle of rational management formulated in two variants: efficiency (maximisation of effect) and economy (minimisation of input).

Performance measurement is a crucial issue for any organisation, regardless of whether it is profit-driven (applicable to business organisations) or not (non-profit organisations) (Kao et al., 2011). Measuring the performance of sports organisations, particularly sports clubs, makes it possible to evaluate their performance against other clubs performing in the same competition class. This comparison is made by confronting performance with competitors (benchmarking). In the literature, the following three methods are used to measure the effectiveness of sports clubs, mainly professional ones: indicative, parametric, and non-parametric. In the first group of methods, financial indicators, e.g. profitability, liquidity, efficiency, debt and others, are used to measure efficiency. These indicators, calculated based on financial statements, i.e. balance sheet, profit and loss account, and cash flow statement, become the basis for comparisons over time and with other clubs operating in the same competition class.

However, due to the specificity and nature of the activities of sports clubs, more than the use of indicator analysis to assess the performance of clubs may be required. This is due to the following reasons. Firstly, most sports clubs, especially football clubs, are characterised by poor financial health. Only a few generate positive economic results, which has a direct impact on achieving profitability or liquidity. Secondly, to survive, clubs conduct business in different markets, i.e. the sports market and the advertising and sponsorship market. In the case of the former market, the recipients of sports product sales are individual consumers, while in the latter market, they are institutional consumers. However, the revenues generated from sports activities (ticket sales, broadcasting revenues, sponsorship and advertising) for clubs, even those in the highest competition classes, must be more significant to ensure financial stability. Compared to sports leagues in Western Europe, in Poland, we observe a situation in which sports clubs, especially from the higher leagues, without financial support from the state and local governments, could not survive (Wyszyński, 2021, 2023). Thirdly, the indicator approach does not allow the multiple dimensions of a sports club’s activities to be considered simultaneously. Often, the calculated financial indicators form two, three, or four variables that become the basis for a selective economic evaluation of the club.

The limitations and inadequacies of the indicator approach lead to a search for methods of measuring the effectiveness of sports clubs that provide a complete view of the measurement issue and, simultaneously, minimise the shortcomings of indicator methods. Currently, research increasingly uses methods that examine the performance of different types of organisations using a production frontier determined based on entities identified as ‘best in practice’. To estimate this frontier, the most common assumption is that the enterprise minimises the consumption of inputs necessary for a given production level. In this case, we speak of input orientation. In contrast, effects are maximised for a given level of inputs in an effects orientation. The methodology of the efficiency-productivity frontier distinguishes between two main methods: parametric and non-parametric. Parametric methods involve determining efficiency from stochastic and non-stochastic quantitative econometric models. Afriath (1972) is the founder of the modern parametric methods approach. The group of these methods includes SFA (Stochastic Frontier Analysis, TFA (Trick Frontier Approach), COLS (Corrected Ordinary Least Squares), FPF (Frontier Production Function) and others. In the group of non-parametric methods, efficiency is established based on models in which no prior knowledge of the parameters that express the relationship between effects and inputs is required. The expenditures incurred by the unit under study enable the achievement of specific (selected) effects from the activity. At the same time, inputs and effects can be expressed in monetary, physical, and other units. These methods primarily include DEA (Data Envelopment Analysis) methods. Among the most important are the following models of this method: CCR – Charnes, Cooper and Rhodes, BCC – Charnes, Cooper and Rhodes, SE-DEA (super efficiency DEA – Banker, Gilford, Andersen, Petersen), NR-DEA (non-radial DEA – non-radial efficiency model), and others. Based on the research, two models, i.e. CCR and BCC, will be described later in this article.

The CCR model proposed in the second half of the 1970s by the three Americans Charnes, Cooper, and Rhodes (1978), has now become one of the most popular non-parametric models used to determine the relative efficiency of economic objects. Efficiency here meant the ratio of the sum of weighted effects to the sum of weighted inputs. This is how the DEA method was born as a frontier data analysis model. As mentioned earlier, the measure of technical efficiency in the DEA method is taken as the Debreu-Farell measure, the original definition which defines it as the difference between level 1 and the maximum possible reduction in inputs at which it is technologically feasible to produce a specific size. Defined in this way, efficiency takes on values in the interval (0,1). In DEA methods, no knowledge of the form of the efficiency function is required. The weights that maximise efficiency are sought using the empirical magnitudes of the variables in the form of inputs and effects (for a given object, DMU – Decision-Making Unit). This results in a mathematical programming task in which the objective is to determine the efficiency of the objects relative to their entire group.

In the literature, efficiency assessments are often made for professional football clubs or professional sports leagues in the USA. In the case of football, the DEA method has been used, among others, by Haas (2003a, b) to determine the efficiency of US-Canadian MLS (Major et al. – a professional football league located at the highest level of competition in the United States and Canada) and English Premier League clubs. In addition to these, DEA method profiles have been used to assess the efficiency of the following league clubs: the Spanish league (Gonzalez-Gomez & Picazo-Tadeo, 2010), German Bundesliga clubs (Haas et al., 2004), French Ligue 1 (Jardin, 2009) and the Polish league (Wyszynski, 2016). We can find research results on the efficiency of sports clubs using parametric methods in the works of Barros and Leach (2006b) and Hofler and Payne (1997), among others. Using the Cobb-Douglas function, they determined the efficiency of clubs in the English Premier League football league and the US National Football League (NFL). In contrast, the application of the Stochastic Frontier Approach (SFA) parametric method to determine the efficiency of English football clubs can be found in the work of Dawson et al., (2000), Barros and Garcia-del-Barrio, (2008), Boto-García et al., (2023).

Problems related to the efficiency of professional sports clubs require an understanding of the specifics of the production process, where managers have to deal with several of its peculiarities. The constructed production function has financial and sporting outcomes on the output side (effects). On the input side (inputs), there are resources and investments for the team. Consequently, the role of football managers can be described as making strategic decisions to convert resources into financial and sporting outcomes in the most efficient way.. In the literature, as a function of the goal of the production process of a professional football club, researchers assume profit maximization (Neale, 1964; Vrooman, 1995; Fort and Quirk, 1995) or win maximization (Késenne, 1996; Quirk and El Hodiri, 1974; Sloane, 1971). On the resources and investments side of the input side of the production function of a sports club, the costs of player salaries, transfer fees and the team’s market value, as determined by player values, are assumed. On the output side, financial results (profits/losses) and sporting results are considered in several points and ranking in the league table. Economic performance depends on the talent of the players (Espitia-Escuer and Garcia-Cebrián, 2010; Fort & Quirk, 1995), while sporting performance depends on the investment of the team in the form of player salaries and transfer payments (Késenne, 1996; Leach & Szymanski, 2015; Szymanski and Smith, 1997). Szymanski (2011) showed that salaries and transfer payments are more or less proportional and suggested that they can be used interchangeably to measure sporting performance.

Data and method

The research covered 12 enterprises operating professional volleyball clubs in the PlusLiga in the 2020/2021 season. The enterprises subject to the analysis conduct business activities and are registered as commercial code companies (joint-stock or limited liability companies). The Polish volleyball league is interesting because of the clubs’ sporting successes on the international stage and the existence of a diverse ownership structure. In addition to private enterprises and associations, clubs are controlled by state enterprises and state and local government companies.. This specificity should be borne in mind when interpreting the results. The full names of the companies, the names of the clubs, and the ownership structure as of 31 December 2021 are shown in Table 1.

Table 1: Club data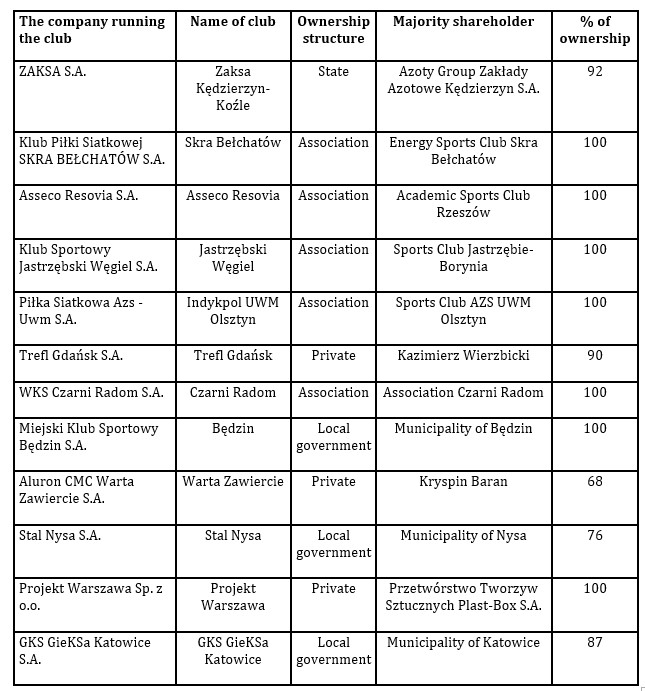

Source: Author’s study based on data from the financial statements of companies

The DEA method was used to determine efficiency, which involves solving a series of linear programming tasks to calculate the values of technological efficiency coefficients (technical, θ_o) under given constraining conditions. The models presented in this paper are referred to in the literature as input oriented CCR and BCC.

Its objective function is to minimise the input level multiplier (Guzik, 2009):

If one assumes:

Constant economies of scale—no condition on L_o—are dealt with by the CCR—CRS (constant return to scale) model. Variable economies of scale occur when L_o = 1, and this is handled by the BCC—VRS (variable return to scale) model.

The solution to tasks (1) – (4) consists in finding the value of the coefficient θ_o, which will allow such a maximum reduction of inputs, at which it will still be possible to achieve a given level of results. Analyzing the studied set of objects requires the formulation and solution of one DEA task for each object, which postulates finding the optimal way of converting the studied object’s inputs into outputs, i.e. finding the optimal production technology. The optimal technology minimises the inputs to a level not exceeding the actual inputs, at which it is possible to obtain results no worse than the actual ones – as determined by the limiting conditions. The θ_o obtained from solving this task is the technological efficiency factor.

In the CCR model with fixed scale effects, a possible proportional reduction in inputs is determined while maintaining at least the same number of outputs. In contrast, the BCC model determines how much less input could produce the same number of effects. It differs from the CCR model’s assumption of variable scale effects by introducing an additional convexity constraint, i.e. L_o = 1. The solution of the CCR model is the so-called total technical efficiency, while the BCC is the so-called pure technical efficiency. When interpreting the results of the optimal solution for the CCR and BCC models, two situations can be distinguished:

1. when the optimum multiplier θ_o is less than 1, the optimum standard technology inputs needed to achieve such results as observed in the facility under study are no more significant than the inputs incurred by the facility. This means that the facility is not fully efficient. The difference 1- θ_o determines the degree of its inefficiency_.
2. when the optimum multiplier θ_o = 1, the optimum expenditures needed to obtain such results as occurred in the studied object are the same as the actual expenditures of this object. This means that the object under study is efficient.

Solving either the CCR or the BCC model does not provide a way of ranking facilities, particularly fully efficient facilities whose efficiency ratios are equal to one. Andersen & Petersen (1993) and Tone (2002) announced a suitable proposal to solve this problem. Based on their proposed CCR model with the so-called super-efficiency (SE-CCR, super-efficiency), the order of football clubs was determined from least to most efficient.

To calculate efficiency measures, the categories of inputs and outputs were selected using a literature review of research on the efficiency of sports clubs worldwide (Wyszyński, 2017) and the production process of a professional sports club (literature). In the production process, variables in the form of investments in the team, i.e., player salary costs or the team’s market value, are assumed to be inputs. Due to the availability of information, one variable was considered to describe the input category, i.e. costs from operations. Three categories of variables were included in the effects: the financial result from operations before interest and taxes (EBIT), the number of points at the end of the regular season, and the final place in the league table. The input and effect categories and the Pearson correlation adopted for the study are shown in Tables 2 and 3. 

Table 2: Categories of inputs and outputs of PlusLiga clubs

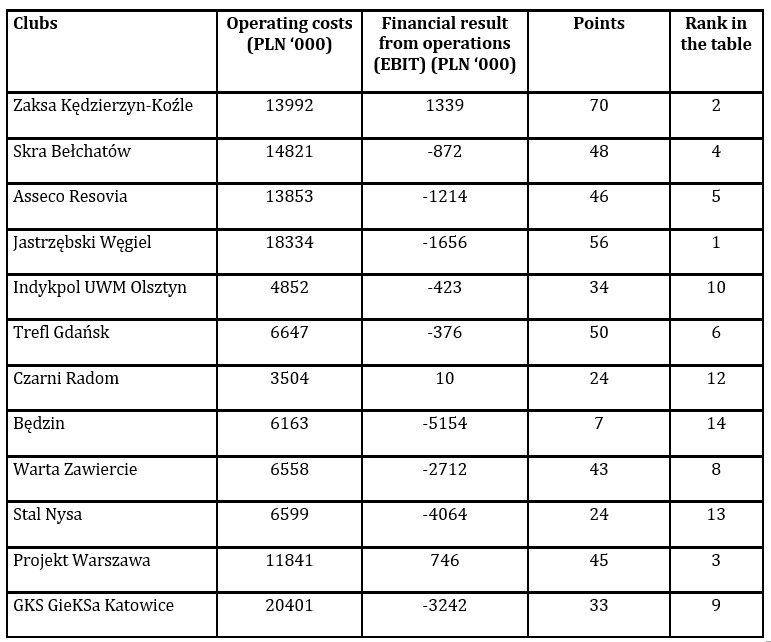Source: Author’s study

Table 3: Pearson correlations between effort and effects

The marked correlation coefficients are significant with p <.05

Source: Author’s study

To carry out the analysis, reliable data from the annual financial statements, reports from the Board of Directors, and additional information published on the website of the National Court Register (https://ekrs.ms.gov.pl/rdf/pd/search_df.) were used. Sports performance data (number of points scored at the end of each season and placed in the table) were sourced from the plusliga.pl website (https://www.plusliga.pl/statsTeams.html). The performance measures of the three CCR, BCC, and SE CCR models of the DEA method were calculated using the linear optimisation programme EMS.

The efficiency of PlusLiga clubs and possibilities for improvement – research results

Table 3 shows the order of the PlusLiga clubs in the league table at the end of the 2020/2021 season, the values of the performance indicators, and the benchmarking formulas (coefficients) of lambda λ_oj (calculated for the CCR model).

Table 4: Results of the technical efficiency assessment of PlusLiga clubs for the 2020/2021 season

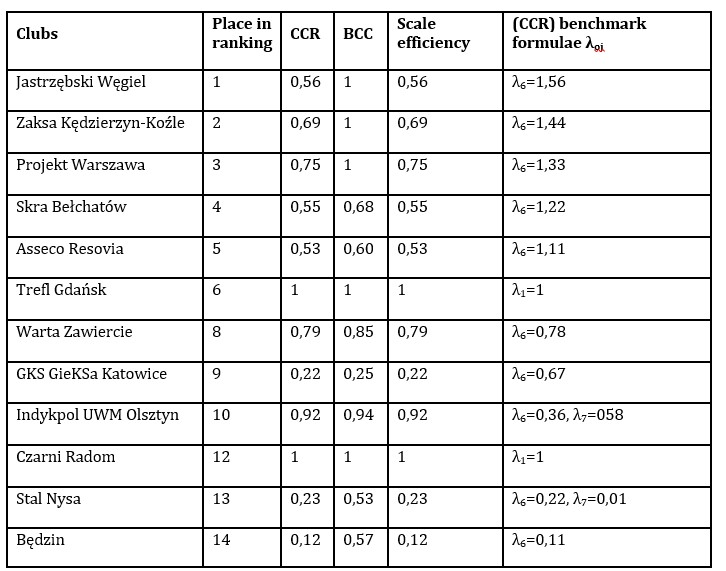
Source: Author’s study

Based on the research, the fully effective clubs (CCR model) in the 2020/2021 PlusLiga season are Trefl Gdańsk and Czarni Radom. The value of the efficiency indicator for the clubs is one (100%), which means that they are efficient both technologically and in terms of the scale of results generated. Given a pure efficiency value of one, Jastrzębski Węgiel, Zaksa Kędzierzyn-Koźle and Projekt Warszawa are technologically efficient under the assumption of variable scale effects (BCC model). Due to the situation where the efficiency (or inefficiency) of these clubs with fixed and variable effects does not match, scale efficiency was additionally determined (Table 3). Based on this, it is possible to decide how much less input could be used if the size of the results were optimal. The measure of scale efficiency took values smaller than unity, which suggests that these clubs were inefficient in the scale of resources involved. The least efficient clubs in Plus Liga are those majority-owned by local governments: Będzin, GKS Katowice and Stal Nysa. These clubs’ technical efficiency (CCR) is only 0.12, 0.22 and 0.23 (see table 2). This implies a need for cost restructuring in the clubs from Będzin and Nysa.

The results of the research presented so far have made it possible, above all, to distinguish effective and ineffective clubs. However, they do not provide the possibility of unequivocally determining the order of clubs regarding the effectiveness achieved (it is about the units considered effective in the group). The application of the SE-CCR model provides such a possibility. The obtained magnitudes of the efficiency indicators calculated based on this model provide the basis for developing the order of clubs in the ranking from the most efficient to the least, as illustrated in Figure 1.

Fig. 1. Ranking of the PlusLiga clubs regarding their efficiency (SE-CCR model)

Source: Author’s study

The most efficient clubs in a group of 12 PlusLiga volleyball clubs are Czarni Radom and Trefl Gdańsk. To achieve their results (amount of operating profit, number of points scored, place in the table), the clubs from Radom and Gdańsk need, respectively, 1.5 and nearly 1.3 times less expenditure than the other clubs in their optimal standard technology. The remaining clubs are not efficient, as their efficiency indicators (ranking coefficients) are below unity..  The competitors of the least efficient PlusLiga club would perform the task at a cost of approximately 12% of the club’s actual expenditure.  The competitors of the least efficient PlusLiga club (Będzin) would perform the task at a cost of approximately 12% of the club’s actual expenditure. 

Based on the efficiency measurement, it is possible to determine the surplus (excess) of operating costs relative to the actual demand, ensuring the volleyball club’s effective functioning with the assumption of fixed effects. Taking this into account, the calculated efficiency measures of the operation of individual sports clubs were used to exemplify the optimum size of salaries and thus identify opportunities to improve the operation of clubs identified as inefficient (Table 5).

Table 5: Results of salary cost optimization for inefficient clubs

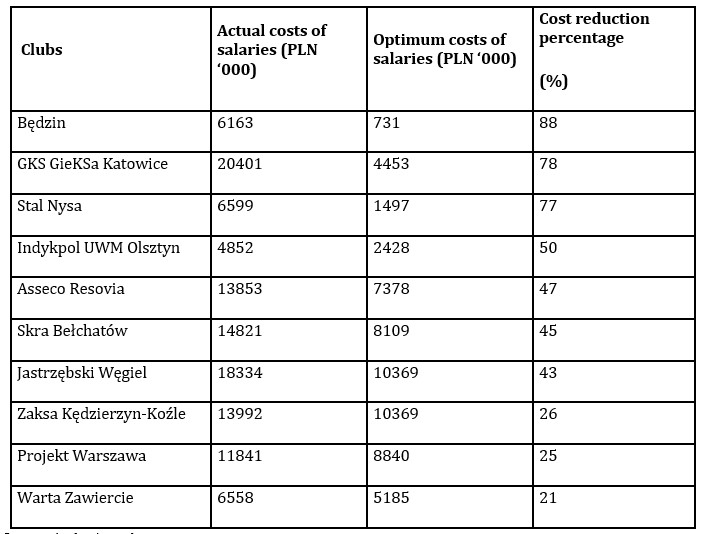Source: Author’s study

The results of the least effective clubs, i.e. Będzin, Stali Nysa, and GKS Katowice, suggest a cost reduction of 77% to 88%, considering the scale of effects achieved and the optimal use of resources. Clubs on whose technologies the inefficient clubs can model themselves (benchmarking formulae λ_oj —Table 2) are Czarni Radom and Trefl Gdansk. They appear in most formulas for inefficient clubs using the CCR model.

An essential element of the effectiveness of professional sports clubs is comparing the size of costs, including personnel costs (salaries of players and coaching staff), to the generated revenue. From the point of view of financial risk and rationality of spending, the costs of clubs should not be higher than the revenues generated. They are exceeding this limit, resulting in a financial loss. Consequently, to continue operations in future periods, the club should find funds to cover the loss shown at the end of the accounting period.  If the intended sporting and economic results are not achieved in the future, the stability and financial security of the sports club may be affected. Therefore, the ratios of the share of operating costs to net sales revenue were calculated for the PlusLiga clubs studied, as shown in Figure 2.

Fig. 2. Operating costs to net revenue ratio of PlusLiga clubs (%)

Source: Author’s study

Three of the 12 clubs surveyed have the lowest operating costs to revenue ratio: Czarni Radom, Zaksa Kędzierzyn-Koźle, and Projekt Warszawa. At these clubs, the ratio is below 100%. By far, the highest proportion of the examined relationship was recorded at clubs from Katowice and Będzin, where costs are more than six times higher than net revenue. The results suggest that these two clubs, the local government’s majority shareholder, generate low net revenues about costs. A professional sports club’s net revenues include those strictly from sporting activities, including ticket sales, funds from sponsors and advertisers, commercial activities, television rights sales and other revenues. To balance the budget, GKS Katowice, Stal Nysa, and Będzin receive funds from the city budget through sponsorship agreements to promote the city, region, public subsidies, capital injections in the form of capital injections and loans and share issues.

Summary

Based on the research carried out, it was found that the operational efficiency of the clubs varies. More than half of the (inefficient) clubs have too high expenses (operating costs) to the actual financial and sporting results. The analysis shows that a low ratio of the costs to net revenue significantly impacts increasing technical efficiency. This suggests that the technology of efficient clubs is primarily based on generating considerably higher revenues relative to the costs incurred. This allows clubs to convert inputs into outputs more efficiently than inefficient ones. Inefficiency was mainly observed in clubs whose majority shareholder is local government. They generate negative financial results. They use budget funds from their owners to cover losses and maintain economic stability. Research suggests that the financial goal of local government clubs is to survive in the market. They operate under soft budget constraints (Kornai, 2003) and are favoured by local governments, which keep them from going bankrupt. It can be assumed that clubs controlled by local governments pursue other goals besides financial and sporting ones, which may contribute to lower efficiency.

The highest efficiency was observed in clubs with majority ownership by private individuals, companies, and associations. Examples are the clubs from Gdansk and Radom, which can best convert the entrusted funds into operating profit (EBIT).

It should also be noted that it is not always the fully effective clubs that occupy the top spots in the league table. In the case of the Polish league, Trefl Gdańsk and Czarni Radom, efficient clubs, occupy places in the middle and lower part of the table. This is confirmed by studies by other authors for other leagues, such as professional football clubs (Haas 2003a, b, Jardin 2009; Barros & Leach, 2006). However, it should be noted that the study was conducted on a sample of clubs for one season of competition. This is mainly related to the availability of information, which clubs in Poland are reluctant to share. Undoubtedly, greater access to economic and financial data would enrich the analysis of the effectiveness of the operation of sports clubs in Poland. Nevertheless, the analysis and observations made in the article can serve as an essential signal for sports club managers as well as the licensing committee of the sports association issuing permission for the club to participate in league competitions. The data from the ranking, developed based on the SE-CCR model, can be one of the essential tools supporting the process related to monitoring the financial situation. This is a potential future direction for research into assessing the effectiveness of sports clubs.

Notes

BCC.: The names are derived from the authors’ surnames: CCR – Charnes, Cooper, Rhodes, BCC – Banker, Charnes, Cooper.

SE-CCR: A detailed description of the SE-CCR model methodology in publications: m.in. Andersen, P. and Petersen NC. (1993), Tone, K. (2002) and Guzik, B. (2008).

Place in the table:   For the determination of correlations and in the DEA analysis, place was taken in an inverse manner, e.g. place 1 was assigned 14, etc.

EMS: The programme is made available on the website of the University of Dortmund, http://wiso.unidortmund.de/LSFR /OR/scheel/ems.

References

• Afriat, S N. (1972), ‘Efficiency Estimation of Production Functions,’ International Economic Review, 13 (3), 568–598. https://doi.org/10.2307/2525845
• Andersen, P and Petersen, NC. (1993), ‘A Procedure for Ranking Efficient Units in Data Envelopment Analysis,’ Management Science, 39 (10), 1261–1264. http://www.jstor.org/stable/2632964
• Banker, RD., Charnes, A. and Cooper, WW. (1984), ‘Some models for estimating technical and scale inefficiencies in data envelopment analysis,’ Management Science, 30 (9), 1078–1092. http://doi.org/10.1287/mnsc.30.9.1078.
• Barros, CP and Leach, S. (2006), ‘Analyzing the Performance of the English F.A. Premier League with an Econometric Frontier Model,’ Journal of Sports Economics, 7 (4), 391-407. https://doi.org/10.1177/1527002505276715
• Barros, CP and Garcia-Del-Barrio, P. (2008), ‘Efficiency measurement of the English football Premier League with a random frontier model,’ Economic Modelling, Elsevier, vol. 25 (5), 994-1002, September. https://doi.org/10.1016/j.econmod.2008.01.004
• Boto-García, D., Varela-Quintana, C, and Muñiz, A. (2023), ‘Foreign players, team production, and technical efficiency: Evidence from European soccer,’ Bulletin of Economic Research, Wiley Blackwell, vol. 75 (4), 1209-1241, October. https://doi.org/10.1111/boer.12407
• Cameron, K. (1986), ‘A Study of Organizational Effectiveness and Its Predictors,’ Management Science, 32, 87-112. http://dx.doi.org/10.1287/mnsc.32.1.87
• Charnes, A., Cooper, WW. and Rhodes, E. (1978), ‘Measuring the efficiency of decision-making units,’ European Journal of Operational Research, 2, 429–444. http://doi. org/10.1016/0377-2217(78)90138-8.
• Dawson, P., Dobson, S. and Gerrard, B. (2000), ‘Stochastic Frontiers and the Temporal Structure of Managerial Efficiency in English Soccer,’ Journal of Sports Economics, 1 (4), 341-362. https://doi.org/10.1177/152700250000100402
• Espitia-Escuer, M. and García-Cebrián, LI. (2010), ‘Measurement of the efficiency of football teams in the Champions League,’ Managerial and Decision Economics, 31 (6), 373–386. https://doi.org/10.1002/mde.1491
• Fort, R. and Quirk, J. (1995), ‘Cross-Subsidization, Incentives, and Outcomes in Professional Team Sports Leagues,’ Journal of Economic Literature, 33(3), 1265–1299. http://www.jstor.org/stable/2729122
• Gonzalez-Gomez, F. and Picazo-Tadeo, AJ. (2010), ‘Can We Be Satisfied With Our Football Team? Evidence From Spanish Professional Football,’ ThE Papers 08/11, Department of Economic Theory and Economic History of the University of Granada.
• Guzik, B. (2008), ‘Zastosowanie modelu SE-CCR do ustalania struktury i siły konkurencji technologicznej,’ [Application of the SE-CCR model to determine the structure and strength of technological competition],’Wiadomości Statystyczne, 2008, nr 10, 15-29. Retrieved from: https://dbc.wroc.pl/Content/39335/PDF/boid_19_2009_1_055_075.pdf
• Haas D.J., Kocher MG. and Slitter, M. (2004), ‘Measuring Efficiency of German Football Teams by Data Envelopment Analysis,’ Central European Journal of Operations Research, 12, 251-268.
• Haas, DJ. (2003a), ‘Technical Efficiency in the Major League Soccer,’ Journal of Sports Economics, 4(3), 203-215. https://doi.org/10.1177/1527002503252144
• Haas, DJ. (2003b), ‘Productive Efficiency of English Football Teams: A Data Envelopment Analysis Approach,’ Managerial and Decision Economics, 24(5), 403–410. http://www.jstor.org/stable/30035596
• Hoefler, RA. and Payne, JE. (1997), ‘Measuring efficiency in the National Basketball Association,’ Economics Letters, 55, 293–299. https://doi.org/10.1016/S0165-1765(97)00083-9
• http://wiso.unidortmund.de/LSFR /OR/scheel/ems
• https://www.plusliga.pl/statsTeams.html
• Jardin, M. (2009), ‘Efficiency of French football clubs and its Dynamice,’ MPRA Paper 19828, University Library of Munich, Germany, 23. June 2009. Retrieved from: https://ideas.repec.org/p/pra/mprapa/19828.html
• Kao, LJ., Lu ChJ. and Chiu, ChCh. (2011), ‘Efficiency measurement using independent component analysis and data envelopment analysis,’ European Journal of Operational Research, Volume 210, Issue 2, 2011. https://doi.org/10.1016/j.ejor.2010.09.016
• Késenne, S. (1996), ‘League management in professional team sports with win-maximizing clubs,’ European Journal for Sport Management, 2(2), 14-22.
• Kornai, J., Maskin E. and Géard, RG. (2003), ‘Understanding the Soft Budget Constraint,’ Journal of Economic Literature, 41 (4): 1095-1136. Retrieved from: https://www.aeaweb.org/articles?id=10.1257/002205103771799999
• Leach, S. and Szymanski, S. (2015), ‘Making money out of football,’ Scottish Journal of Political Economy, 62 (1), 25–50. https://doi.org/10.1111/sjpe.12065
• Matwiejczuk, R. (2000), ‘Efektywność – próba interpretacji,’[Efficiency – an attempt at interpretation],’ Przegląd Organizacji, (11). Retrieved from: https://przegladorganizacji.pl/plik/5e092493ca183/po.2000.11.05.pdf
• Matwiejczuk, R. (2006), Zarządzanie marketingowo-logistyczne. Wartość i efektywność. C.H. Beck.
• Neale, WC. (1964), ‘The Peculiar Economics of Professional Sports,’ The Quarterly Journal of Economics, Volume 78, Issue 1, February, Pages 1–14, https://doi.org/10.2307/1880543
• Quirk, J. and El Hodiri, M. (1974), ‘The economic theory of a professional sports league,’ Government and the sports business, vol 33, 53.
• Samuelson P A. and Nordhaus W. D. (2004), Ekonomia, Wydawnictwo Naukowe PWN.
• Sloane, PJ. (1971), ‘The economics of professional football: The football club as a utility maximiser,’ Scottish Journal of Political Economy, 18 (2), 121–146. https://doi.org/10.1111/j.1467-9485.1971.tb00979.x
• Sznajder A. (2012), Marketing sportu, Wyd. PWE, Warszawa.
• Szymanski, S. and Smith, R. (1997), ‘The English Football Industry: Profit, performance and Industrial Structure,’ International Review of Applied Economics, 11(1), 135-153, https://doi.org/10.1080/02692179700000008
• Szymanski, S. (2011), ‘Wages, transfers and the variation of team Performance in the English Premier League,’ Paper prepared for the VI Gijon conference on sports economics. https://doi.org/10.4337/9781781002865.00011
• Szymanski, S. and Smith, R. (2010), ‘The English football industry: Profit, performance, and industrial structure,’ International Review of Applied Economics, 11(1), 135–153.
• The Sports Act of 25 June 2010. https://isap.sejm.gov.pl/isap.nsf/download.xsp/WDU20101270857/U/D20100857Lj.pdf
• Tone, K. (2002), ‘A slacks-based efficiency measure in Data Envelopment Analysis,’ European Journal of Operational Research, 143, pp. 32-41. https://doi.org/10.1016/S0377-2217(01)00324-1
• Vrooman, J. (1995), ‘A General Theory of Professional Sports Leagues,’ Southern Economic Journal, 61(4), 971–990. https://doi.org/10.2307/1060735
• Wyszyński, A. (2016), ‘Efficiency of Football Clubs in Poland,’ Olsztyn Economic Journal, 11(1), 59–72. https://doi.org/10.31648/oej.2902
• Wyszyński, A. (2017), ‘Efektywność klubów piłkarskich w Polsce,’ [Efficiency of Football Clubs in Poland],’ Ekonomista [Economist], (3), 294-322. Retrieved from https://archiwum.pte.pl/pliki/1/8905/Ekonomista2017-3_59-87.pdf
• Wyszyński, A. (2021), ‘Form of ownership and economic and sports results of football clubs in Poland,’ Journal of Physical Education and Sport, 21(2), 1142–1149. https://doi.org/10.7752/jpes.2021.s2144
• Wyszyński, A. (2023), ‘Financial and Sports Results of Public Sector Enterprises Operating Professional Sports Clubs,’ Olsztyn Economic Journal, 18(1), 23–37. https://doi.org/10.31648/oej.9429