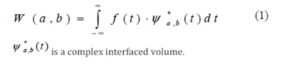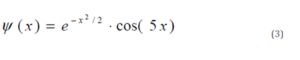Similar results were acquired by Studwell (2013), who emphasized the need to control the financial sector in order to grow, and named liberalization of financial sector one of the most important obstacles for economic growth — in the case of the most promising Asian economies. Both studies outline the role of the financial sector and seem to overthrow the dominance of Fischer’s equation: if not controlled, the financial sector can grow much bigger and suppress the real sector. Still, both studies prove the fact, but do not shed light on the origins of such interactions between financial and real sectors.
In the study of 2014 (Svirina et al., 2014), it is proposed that the stage of the economic cycle at a time point can be defined on the basis of the ratio between the financial and real sectors of the economy. A growth stage is observed when there is parity between those sectors, which means that the amount of consumption within the economic system is equal to the amount of investment. A recession begins when the financial and real sectors become highly unbalanced — and this comes in line with the findings of Cecchetti and Kharroubi who captured the quantitative proof of such misbalance.
Putting together these findings, we suggest that the phenomenon Cecchetti and Kharroubi (2015) are observing relates to the end of the economic cycle, and indicates that currently the disproportion between financial and real sectors is large enough to say we are in the world of quantum economy. We have tested this hypothesis both with statistical analysis and using wavelet transform: the results can be found below.
Literature review
Theoretical methodologies addressing and incorporating economic cycles (and economic crises as a part of economic cycle) were designed to explain typical economic fluctuations over time and to systematize the diverse and inconsistent retrospective data on economic development. Currently, there are a number of theories premised upon economic cycles that analyze problems ranging from global economic development to single enterprise development. Their common feature is that they posit that development is cyclical rather than pendular (Hansen, 1951).
The main measuring parameter implemented in cyclical-wave methodology is time, which is seen as the indicator that characterizes a sequence of specific events. According to this parameter, the length of social systems’ cycles can be divided into three groups: the macrolevel, the mesolevel, and the microlevel. Thus, the duration of the “industry cycles” introduced by S. Kuznets (Kuznets, 1965) or the “innovation lifecycle” introduced by J. Schumpeter (Schumpeter, 1939) can vary from a few months to a few decades. Karl Marx’s “cycle of main capital turnover” (Marx, 1990) can last 50-60 (or more) years–the duration of the cycle depends on the period of service that is appropriate for a certain type of main capital.
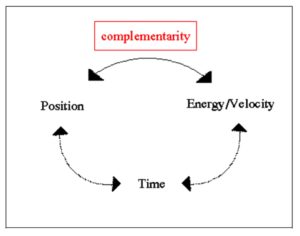
In physics this principle applies to estimation of position and velocity of electron, and an analogue can be found in socio-economic systems when we try to measure the potential (an analogue of energy/velocity) and efficiency (actual position) of socio-economic systems. The main effect retrieved from physics is that if potential or efficiency are fixed in time, one is either unable to measure socio-economic system’s potential or efficiency.
In order to estimate the range of efficiency for resources performance on the basis of acquired data, we performed wavelet transformation on the basis of original signal. According to the recommended procedure (Astafijeva, 1996; Chun-Lin, 2013; Mallat, 1998), continuous wavelet transform is carried out by convolution of the analyzed signal (function) from two-parametrical wavelet function (se Eq. 1).
The basis of wavelet transform is derived from the mother wavelet by means of scaling and shifting (see Eq.2).
 a — the large-scale coefficient defining the width of a wavelet, b — the shift parameter defining the provision of a wavelet on an axis t.
a — the large-scale coefficient defining the width of a wavelet, b — the shift parameter defining the provision of a wavelet on an axis t.
Wavelet transform allows to analyze the thin structure of signals as the mobile time-and-frequency window, which equally well marks out low frequency and high frequency signal components and thus have a big advantage over the analysis of signals’ local features — the latter are absent at Fourier’s transformation.
For the purposes of this study, we have chosen Morlet wavelet, which has narrow spectral range and considerable duration in a time domain (see Eq.3):
This mother wavelet suits best the basic purpose of the study as it allows evaluating long periods of time and the narrow range of the basic independent variable.
Main findings
When time is viewed as an independent variable for economic cycle modeling, one should explain why cycles of the same type differ significantly in terms of their duration. For example, a Kondratiev wave can last from 40 to 60 years (Korotayev & Tsirel, 2009). Thus, such models would have little accuracy in predicting the beginning of the next stage or the next cycle because the maximum duration of the cycle is 1.5 times greater than its minimum duration.
Thus, the average error of the prognosis model based on a time-based business cycle model is 51.68%, which is unacceptably high for a model. This leads to a conclusion, that time is possibly only a descriptive statistical measure that can be used to describe economic cycles, and can not be viewed as an independent variable — hence, a predictor which would allow evaluating economic cycles, is necessary.
According to our previous research (Svirina et. al, 2014), conversion point from classical to quantum economy is defined in our opinion by the ratio between the volumes of real and financial sectors of the economy: in case there is parity between those, the laws of classical economy operate; if these sectors are highly disproportional — the laws of quantum economics start operating. This can be formalized in the following way (see Eq.4):
MV = PQ + Ñ’*PQ = PQ * (1 + Ñ’) (4)
where MV — the volume of stock of money and quasi-money (financial aggregates) corrected by the turnover speed of this total stock, monetary units; PQ — the volume of real sector of the economy, defined as a sum of goods and services produced, corrected by the price, monetary units; Ñ’ — parameter, characterizing disproportion between the financial and real sectors of the economy.
Such approach allows eliminating the problem of immeasurability of financial sector volume at a certain time point.
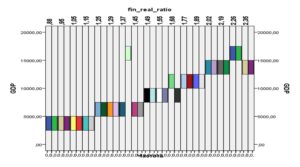
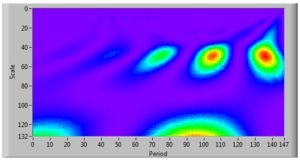
For the purposes of this study we have estimated the ratio between the financial and real sectors of economy volume as a possible predictor of economic crisis, and evaluated the data on the US financial and real sector volumes from 1867 to 2013. GDP was viewed as the volume of real sector, while the financial sector volume was estimated as the turnover of financial institutions and quasi-monetary instruments, acquired from the open source (US Bureau of Census, 2014). The evaluation of this ratio on a time-scale can be seen on Figure 2
As it can be seen from Figure 4, financial/real sector ratio can serve as predictor of major economic crises: on the scalogram at the level of 50 (which evaluates intensity), one can see three visualized versions of the crisis: first one appears from year 60 to 80 (1927-1947) which reflects the Great Depression and the World War II, the red center of the oval-shaped figure which refers to the upcoming Energy crisis, and the final red-centered figure which refers to the economic crisis of 2007-2013. However, the predictor indicates the start of crises at an earlier stage than it had revealed (1927 for the Great Depression, 1967 for the Energy crisis and 2004 for the last financial crisis) — thus, we can consider this predictor to evaluate the upcoming crisis with higher probability than the existing tools. It is also worth mentioning that wavelet transform also allows evaluating intensity: it can be seen from Figure 4 that the last economic crisis appeared to be more intensive than the Great Depression or the Energy crisis.
Thus, we suggest that the economic cycle stage (regarding long term cycles) is defined by the ratio of real to financial sector volumes. A growth stage is observed when there is parity between the two sectors, meaning that the amount of consumption within the economic system is equal to the amount of investment. A recession begins when the financial and real sectors become highly unbalanced; this is in line with the findings of Cecchetti and Kharroubi (2015), who captured the quantitative proof of such imbalance.
One can also notice bigger shapes on 130 levels of intensity, which we consider to be long waves reflecting changes in economic formations, but the limited data which are used for this study do not allow making justified conclusions on the issue.
Discussion and limitations
The first finding of our study, which has theoretical implications, is the suggested quantum approach towards economic crisis possibility estimation, which evaluates the financial sector as the one changing with the level of volatility that can not be explained within deterministic paradigm. The second finding which enriches existing literature in economic crisis evaluation by suggesting to use financial/real sector volume ratio as a predictor of economic crisis along with wavelet transform, which reveal certain tendencies on the global level. The third finding of the paper is the use of wavelet transform to evaluate economic data, which can provide research with the results that can not be identified by traditional methods. Finally, the proposed approach allows foreseeing economic crisis 4-5 years prior to active stage of the crisis, thus the implication to practice is acquiring extra time to prepare for the crisis, and in certain cases to propose regulation changes to avoid major problems in country development.
The main limitation of the study is that we used only the data on the US financial and real sectors of the economy, hence our findings may be relevant only to this country’s economy rather than be a universal trend. The second limitation comes from the sources of data: the financial sector of the US was evaluated between 1967 and 2014, but the structure of this sector, which might affect the estimated volume, had changed significantly during 147 years — hence a few assumptions were made to provide financial volume assessment with the same methodology along this timeline. Though measures were taken to decrease possible mismatches, these could appear and decrease the significance of the findings.
According to the limitations’ state, the following trends for future research can be estimated. First, the findings are to be tested with the data from other countries besides the US along the same timeline. Second, alternative methods of financial sector volume estimation are to be considered to eliminate the possibility of inadequate estimation along the timeline. Third, it should be investigated, what type of crisis appears on the higher levels of intensity, as this possibly might be a change of economic formations.
Further research should also address the time issue and evaluate the possibility that relativity laws from quantum physics also apply to economic situations, thus distorting the understanding of economic agents on the time left to upcoming crises.
Acknowledgement
This research was carried out under Russian Fund for Fundamental Research (RFFI) grant program, grant 14-06-00350 “Evaluation of the hypothesis on possible quantum nature of economic environment and economic cycles”.
References
1. Astafijeva, N.M. 1996. Wavelet analysis: basic theory application examples. Successes in Physical Sciences. No 11, p.1145.- 1170
2. Boero, G., Smith, J., Wallis, K. 2008. Uncertainty and Disagreement in Economic Prediction: The Bank of England Survey of External Forecasters. The Economic Journal, Vol. 118, No. 530, pp. 1107-1127
Google Scholar
3. Cecchetti, S., Kharroubi E. 2015. Why does financial sector growth crowd out real economic growth? Retrived from https://www.bis.org/publ/work490.pdf
Google Scholar
4. Cencini A. 2001. Monetary Macroeconomics. A New Approach. New York: Routledge. pp. 63-84.
5. Chun-Lin, L. 2013. A Tutorial to Wavelet Transform. Retrieved from http://disp.ee.ntu.edu.tw/tutorial/WaveletTutorial.pdf
6. Downey, K., Slocum, J. 1975. Uncertainty: Measures, Research, and Sources of Variation. Academy of Management Journal. No 18. pp. 562-578.
Publisher – Google Scholar
7. Eusepi S., Preston B. 2011. Expectations, Learning and Economic cycle Fluctuations. American Economic Review 101
8. Goncaves, C. 2012. Chaos and Nonlinear Dynamics in Quantum Artificial Economy. 2012. arXiv:1202.6647v1 29Feb2012.
9. Hansen A.H. 1951. Business Cycles and National Income. Norton publishing.
Google Scholar
10. Heisenberg, W. 1927. “Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik”, Zeitschrift für Physik (in German) 43 (3—4): 172—198
Publisher – Google Scholar
11.Jurado, K., Ludvigson, S., Ng, S. 2013. Measuring Uncertainty. Retrieved from
http://www.econ.nyu.edu/user/ludvigsons/vol.pdf
Publisher – GoogleScholar
12. Kondraty’ev N.D. 1989. Problemy Ekonomicheskoy Dinamiki. Moscow: Economica.
13. Kuznets S. 1965. Economic Growth and Structure: Selected Essays. New York: Norton
Google Scholar
14. Lev, B. 1975. Environmental Uncertainty Reduction by Smoothing and Buffering: An Empirical Verification. Academy of Management Journal. No 18. pp. 864-871.
Publisher – Google Scholar
15. Lorsch J., Allen S. 1973. Managing Diversity and Interdependence: An Organizational Study of Multidivisional Firms. Boston: Harvard University Graduate School of Business Administration, Division of Research
16. Mallat, S. 1998. A wavelet tour of signal processing. Academic Press
17. Marx K. 1990. Capital: Critique of Political Economy. London: Penguin Books
18. Schumpeter J. 1939. Economic cycles: A theoretical, historical and statistical analysis of the Capitalist process. Eastford: Martino Publishing
19. Sobey C. 2012. A Model of Quantum Economic Development. http://mpra.ub.uni-muenchen.de/36422/
20. Studwell J. 2013. How Asia Works. London: Profile Books.
21. Svirina A., Parfenova E., Shurkina E. 2014. The Nature of Business Cycles: a Quantum Approach. Proceedings of 24th International Business Information Management Association Conference, Milan, Italy, November 6-7, 2014. pp. 755-763.
22. Sweeney, W., Kenyon, D., Kramer, R. 1987. Toward an Appropriate Measure of Uncertainty in a Risk Programming Model. American Journal of Agricultural Economics, Vol. 69, No. 1, pp. 87-96
Publisher – Google Scholar
23.Ternyik S. 2012. The Monetary Quantum. 2012. http://mpra.ub.uni-muenchen.de/41973/
Google Scholar
24. Uncertainty principle. 2013. Retrieved from: http://abyss.uoregon.edu/~js/21st_century_science/lectures/lec14.html
25. US Bureau of Census. 2014. Historical Statistics of the United States. Federal Reserve Bank at St.Louis.